Cosma Shalizi Research

Maximum Likelihood Estimation for q-Exponential (Tsallis) Distributions

The q-exponential distributions are a special case of the type II generalized Pareto distribution; they were introduced into the literature of statistical mechanics by Constantino Tsallis, who argued, on theoretical grounds, for their applicability to systems with long-range interactions. They have come to be used more generally by physicists to model the distribution of many heavy-tailed phenomena in complex systems. While I have my doubts about all this, if people are going to fit them to data they ought to fit them well, and that means using maximum likelihood estimates.

Relevant files:

"Maximum Likelihood Estimation for q-Exponential (Tsallis) Distributions", math.ST/0701854: A short (4 pp.) paper, showing how the q-exponentials are a special case of one of the generalized Pareto distributions, recapitulating the derivation of the maximum likelihood estimator, and establishing its superiority to the practice of fitting curves to the distribution function.; Last revised 31 January 2007.
tsallisqexp: Tsallis q-Exp Distribution: An R package available through CRAN: Paul Higbie took the initiative to make this happen, and Christophe Dutang actually did the code packaging.

So as not to break links, I still have here my original code, but you should really use the package.

tsal.R

A set of functions, written in R, to do calculations with the q-exponential distributions, to implement the MLE described in the paper, and to do some bootstrap error checking.

Usage information is provided in the comments, which are pretty extensive.

Note that this is not a proper R package, because I am insufficiently motivated to put one together.

This code is free, open-source software, released under the Gnu Public License. You are free to redistribute it or modify it under certain conditions. It comes with absolutely no warranty whatsoever.

Last revised (version 0.2.1) on 6 February 2007.

COPYING_WARRANTY

A copy of the relevant Gnu Public License.

tsal.tgz

A tar'd, gzip'd arxiv containing this document, the paper, the code, the figures below, and the legal documentation.

Installation

(Again, this is all superseded by the package at CRAN.)

Put a copy of tsal.R in your favorite directory. Have R source the file. (From the R command line, this is source("path_to_tsal/tsal.R"), where path_to_tsal is the path from R's current working directory to wherever you put the code.) The functions are now ready for use.

The code contains two functions, plot.tsal.quantile.transform and plot.tsal.LR.distribution, which are intended to sanity-check the quality of the implementation. When run with their default parameters on my laptop, they give the following pictures, respectively (click for higher-resolution PDF versions, about 1.5 Mb):

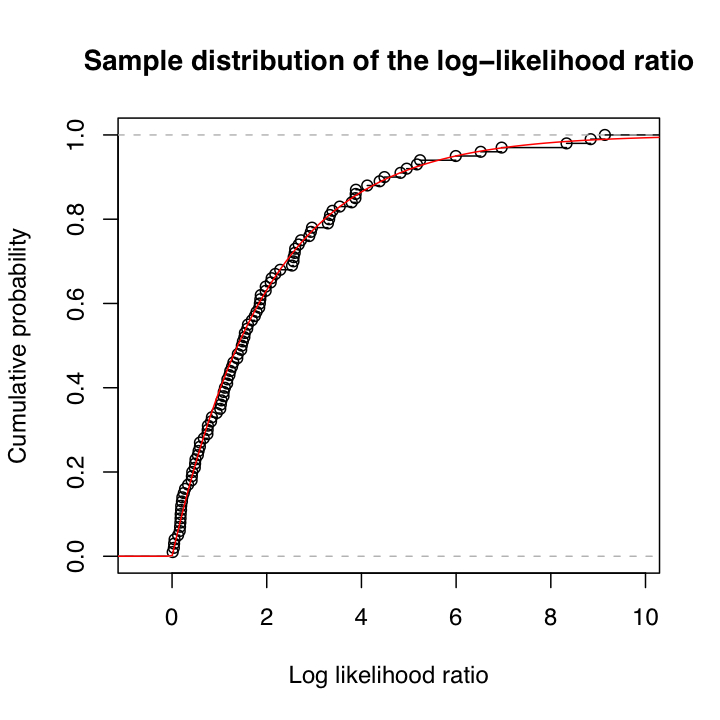
Run on your machine, the results should be similar. (But plot.tsal.LR.distribution calls the random number generator each time it is run, so if you get exactly the same figure, that is also suspicious.)

Page created 28 January 2007, last revised 17 March 2015