Notebooks

Branching Processes

13 Nov 2024 14:41

\[ \newcommand{\Expect}[1]{\mathbb{E}\left[ #1 \right]} \newcommand{\Prob}[1]{\mathbb{P} \left( #1 \right)} \]

A class of stochastic process important as models in genetics and population biology, chemical kinetics, and filtering. The basic idea is that there are a number of objects, often called particles, which, in some random fashion, reproduce ("branch") and die out; they can be of multiple types and occupy differing spatial locations. They can pursue their trajectories and their biographies either independently, or with some kind of statistical dependence across particles.

The most basic version has one type of particle, and no spatial considerations. At each time step, each parrticle gives rise to a random number of offspring; the distribution of offspring is fixed, and the number is independent across time-steps and across lineages (IID). This is the so-called Galton-Watson branching process. Galton introduced it as a model of the survival of (patrilneal) family names, so that only male offspring counted; he required the distribution of time until a given lineage went extinct. This was provided almost immediately by Watson, in a very elegant use of the method of generating functions, which is, itself, reproduced in probability textbooks down to the present day. (However, when I first encoutnered the problem, in a probability class, the teacher presented it as one about the survival of matrilineal lineages, defined by inheritance of mitochondrial DNA. Whether this was conscious subversion of the patriarchy, or just a reflection of the changing scientific interests between the 1890s and the 1990s, I couldn't say.)

Beyond the cases of family lineages (which have obvious biological applications), branching processes show up as tools, representations or approximations in lots of areas of math and of science, including one that may yet doom us all explains why a bunch of the classic studies were funded by the US military.

Sketch of the Galton-Watson Argument, Because It Is So Pretty

Time proceeds in discrete generations. In generation $t$, there are $ X_t $ organisms. Each organism leaves a random number of offspring before expiring itself, say $ Y_{it} $ for t he number of offspring for organism $i$ at time $t$. Thus \[ X_{t+1} = \sum_{i=1}^{X_t}{Y_{it}} \] assuming, of course, that $ X_t > 0 $. (If $ X_t=0 $ then so is $ X_{t+1} $; extinction is forever.) The random offspring numbers $ Y_{it} $ are drawn independently from an (unchanging) distribution $p$, so $p(k)$ is the probability that an individual has $k$ offspring, $\sum_{k=0}^{\infty}{p(k)} = 1$, $p(k) \geq 0$.

It's worth noticing two (related) things about this process at this point:

  1. If we restrict ourselves to the descendants of any given organism in any given generation, we have a new branching process, following exactly the same distribution of offspring $p$ as the original process.
  2. The process $ X_t $ is Markovian: all that matters is the size of the current population, not the history which brought it to that state.

Introduce the abbreviations $\rho=p(0)$ and $\mu=\sum_{k=0}^{\infty}{kp(k)}$, for the probability of leaving no offspring, and for the mean number of offspring. Clearly, $\rho > 0$ is a necessary condition for extinction, and $\mu < 1$ is a sufficient condition for $\rho > 0$. If we ignored random fluctuations and just blindly took averages, we'd anticipate $ X_t = X_0 \mu^t $, which would suggest that $\mu < 1$ implies eventual extinction. This turns out to be true!

Inspired by observation (1) above, let's stick to the case where $ X_0=1 $, i.e., the population starts with a single founder. Let's say that $ \alpha_d $ is the probability that this branching process persists for $\leq d$ generations before going extinct. What we really care about is $ \alpha_{\infty} $, the probability that the process dies out at some time. Notice however that the event "the process persists for $\leq d$ generations before going extinct" includes, as a proper subset, the event "the process persists for $\leq d-1$ generations before going extinct", so $ \alpha_{d} \geq \alpha_{d-1} $. So the $ \alpha_d $s are a non-decreasing sequence; being probabilities, they are also all bounded above by $1$. Thus the limit $ \lim_{d\uparrow\infty}{\alpha_d} $ is well-defined and equals the $ \alpha_{\infty} $ we want. So let us try to get a handle on $ \alpha_d $, and how it grows with $d$.

There are two, mutually exclusive, possibilities for "persisting for $\leq d$ generations before going extinct":

The probability of the first event is $\rho$. Given that the founder left $ X_1>0 $ descendants, the probability of the second event is $ \alpha_{d-1}^{X_1} $, because each of the descendants starts an independent branching process (observation (1) above). Thus we have \[ \alpha_d = \rho + \sum_{k=1}^{\infty}{p(k) \alpha_{d-1}^{k}} \] This suggests a recursion for the extinction-by-generation-$d$ probabilities, which we could write as follows: \[ \begin{eqnarray*} \alpha_d & = & f(\alpha_{d-1})\\ f(x) & = & \rho + \sum_{k=1}^{\infty}{p(k) x^k}\\ \alpha_1 & = & \rho \end{eqnarray*} \]

We can therefore find $ \alpha_{\infty} $ by starting with $ \alpha_1 = \rho $ and iterating: $\alpha_2 = f(\rho)$, $\alpha_3 = f(f(\rho))$, etc. It is easy to check (exercise!) that $f(1)=1$. If $f^{\prime}(1) \leq 1$, this fixed point is stable, so the iteration will converge to it, and the branching process will die out eventually with probability 1. If, on the other hand, $f^{\prime}(1) > 1$, then that fixed point is unstable, and the iteration will converge to the other fixed point, leaving a finite probability of surviving forever. What's that derivative? \[ \begin{eqnarray} f^{\prime}(x) & = & \sum_{k=1}^{\infty}{k p(k) x^{k-1}}\\ f^{\prime}(1) & = & \sum_{k=1}^{\infty}{k p(k)} = \mu \end{eqnarray} \] Thus the branching process is doomed to eventual extinction exactly when $\mu \leq 1$, as promised; if $\mu >1$, it has some probability of surviving forever, which can be found by solving $f(x^*) = x^*$.

Some after-notes:

Some Illustrations

First, have a great heaping hunk of R code (in case anyone is interested): 

# Draw a branching process with k generations
  # Always start from a single ancestor
  # More iteration than is probably ideal in R, but oh well   
# Inputs:
  # Number of generations (k)
    # Assumed to be at least 3
  # Function for sampling from offspring distribution (roffspring)
    # Required that the first argument be n
  # Optional additional arguments to roffspring (...)
# Output: a directed graph, in the format of the "network" object
# Side-effect: network is plotted
# Presumes without checking:
  # roffspring returns non-negative integers
rgaltonwatson <- function(k, roffspring, ...) {
  stopifnot(require(network))
  stopifnot(k>2)
  # Keep track of how big each generation is (k numbers)
  generation.sizes <- vector(length=k) 
  generation.sizes[1] <- 1
 # Track number of offspring per individual by generation (k-1 vectors)
  generation.counts <- list(length=k-1)
  for (t in 2:k) {
    # Randomly draw offspring numbers, one per member of the previous generation
    if (generation.sizes[t-1] > 0) {
      generation.counts[[t-1]] <- roffspring(n=generation.sizes[t-1], ...)
    } else {
       generation.counts[[t-1]] <- 0
    }
    # Sum up for future reference
    generation.sizes[t] <- sum(generation.counts[[t-1]])
  }
  # Label individuals by generation
  generation.labels <- rep(1:k, times=generation.sizes)
  # How many individuals in the total branching process?
  n <- length(generation.labels)
  # Create an adjacency matrix
  adj <- matrix(0, nrow=n, ncol=n)
  # Fill in the adjacency matrix
  for (t in 1:(k-1)) {
    # Who are all the members of that generation?
    senders <- which(generation.labels==t)
    # Who are all the members of the _next_ generation?
    offspring <- which(generation.labels==(t+1))
    # Skip if there aren't any offspring!
    if (length(offspring) > 0) {
       # Parents' positions within the previous generation
       child.of <- rep(1:length(senders), times=generation.counts[[t]])
       for (i in 1:length(senders)) {
          sender <- senders[i]
         receivers <- offspring[which(child.of==i)]
         adj[sender, receivers] <- 1
      }
    }
  }
  # Color nodes by generation
  node.colors <- rep(1:k, times=generation.sizes)
  # Nodes are round, unless they have no children (squares) or are the
  # last displayed generation (triangles)
  out.degrees <- rowSums(adj)
  node.sides <- ifelse(out.degrees > 0, 50, 4)
  node.sides[generation.labels==k] <- 3
  the.network <- as.network(adj)
  plot(the.network, vertex.col=topo.colors(k)[node.colors],
       vertex.sides=node.sides)
  invisible(the.network)
}

Now let us look at some realizations, where the offspring distribution is Poisson, either $\mu=0.9$, $\mu=1$, or $\mu=2$ (corresponding to $\rho=e^{-0.9} = 0.4066$, $\rho=e^{-1} = 0.3679$ and $\rho=e^{-2} = 0.1353$): 

nr <- 4
par(mfcol=c(nr,3))
replicate(nr, rgaltonwatson(k=5, roffspring=rpois, lambda=0.9))
replicate(nr, rgaltonwatson(k=5, roffspring=rpois, lambda=1.0))
replicate(nr, rgaltonwatson(k=5, roffspring=rpois, lambda=2))

From left to right: $\mu=0.9$, $\mu=1.0$, $\mu=2$, all with Poisson distributions for the number of offspring, stopping at 5 generations (if not before). (Nodes which look like they have multiple parents are accidents of the layout algrithm, which I have spent too much time fussing with already.)

What about the function $f(x)$ and its fixed point? For a Poisson distribution, some character-building algebra shows that $f(x)=e^{\mu(x-1)}$. (Exercise!) Now let us plot it: 

par(mfrow=c(1,1))
curve(exp(0.9*(x-1)), from=0, to=1, lty=1, pty="s", ylim=c(0,1), xlim=c(0,1),
      xlab="x", ylab="f(x)")
curve(exp(1.0*(x-1)), add=TRUE, lty=2)
curve(exp(2.0*(x-1)), add=TRUE, lty=3)
abline(0,1, col="grey")
legend("topleft", legend=paste("mu", "==", c(0.9, 1.0, 2.0)),
       lty=1:3)

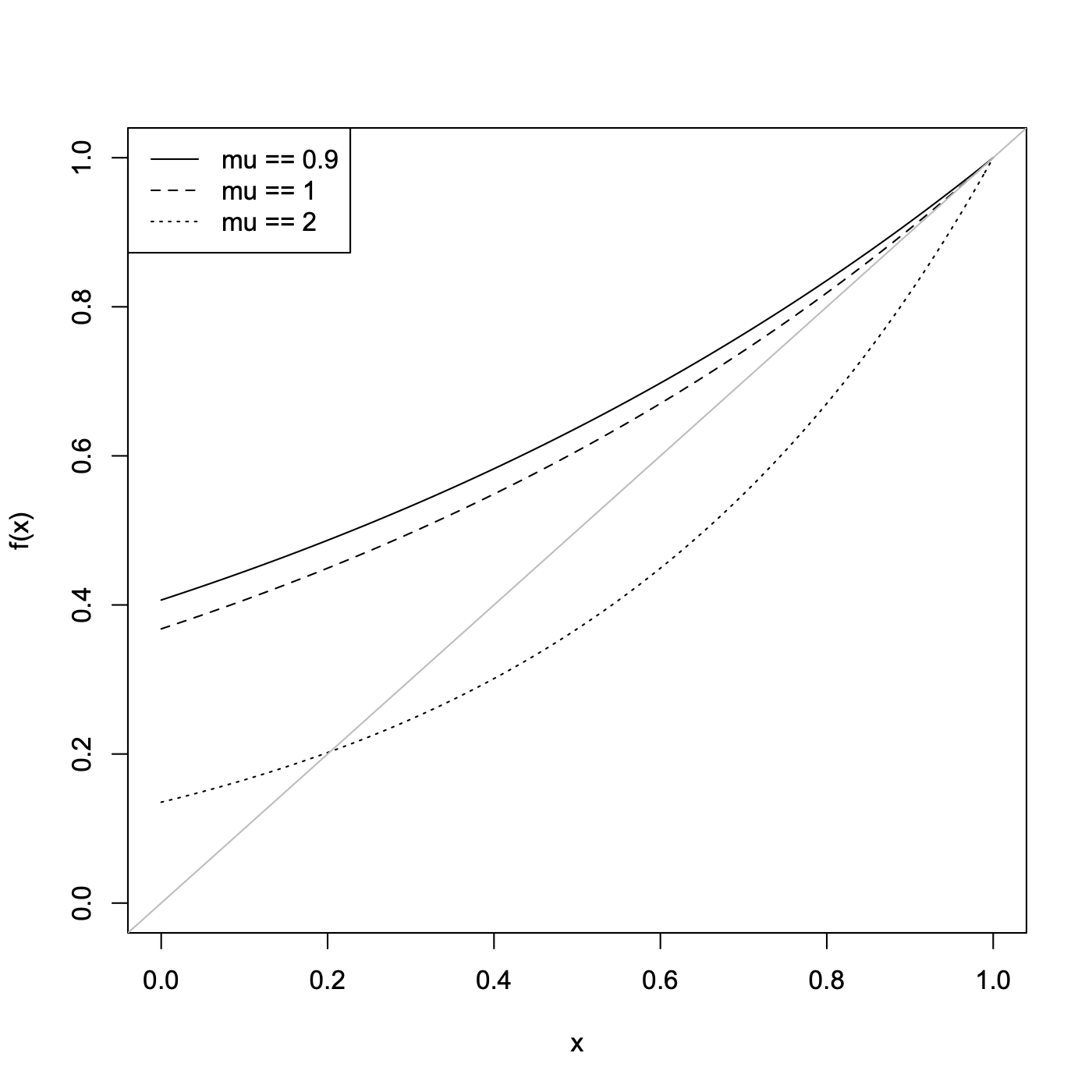
To use these curves to compute the sequence $ \alpha_d $, start at $ \alpha_1 = rho $ on the horizontal axis, draw a vertical line to the $f(x)$ curve, getting $ \alpha_2 $,then a horizontal line to the diagonal (in grey), then a vertical line to the curve again (getting $ \alpha_3 $), and so on. This has to converge to a fixed point, where the curve intersects the diagonal. Exercise: draw these lines for the cases shown.

I will leave as a further exercise to modify the code, and the function $f(x)$, to handle the situation where a node has 0 offspring with probability $\rho$, and (say) 10 offspring with probability $1-\rho$, and compare the results, matching first $\mu$ and then $\rho$ to my Poisson illustrations.

Statistical Inference for Galton-Watson

If we get to observe how many offspring each particle has in each distribution, what I called \( Y_{it} \) above, then statistical inference for the offspring distribution $p$ is easy: each \( Y_{it} \) is an IID sample from $p$, so we can use our favorite technique, parametric or non-parametric as appropriate, for learning distributions from IID data.

If we only get to observe the total population sizes, \( X_t \), then things are suddenly much trickier. As I mentioned, \( X_t \) is a Markov process, so the general theory of statistical inference for Markov processes applies. In particular, the elements of the transition matrix \( \tau_{mn} \equiv \Prob{X_{t+1}=m|X_t=n} \) will dictate the likelihood function, and those elements are in turn dictated by the distribution $p$. Specifically, the probability that the next population size is $m$ when the current population size is $n$ is the probability that $n$ draws from $p$ will add up to $m$: \[ \tau_{mn} = \sum_{y_1, y_2, \ldots y_{n-1}}{\left(\prod_{i=1}^{n-1}{p(y_i)}\right) p(m - \sum_{i=1}^{n-1}{y_i})} \] (with the understanding that $p(k)$ is 0 for negative $k$). This is (basically) convolving $p$ with itself $n$ times. You can imagine how this might get computationally involved.

The form of this distribution also leads to a curious identifiability issue. The central limit theorem tells us that the sum of $n$ IID random variables, each with mean $\mu$ and variance $\sigma^2$, tends towards a Gaussian, $\mathcal{N}(n\mu, n\sigma^2)$. (If you find that an unacceptably sloppy statement of the CLT, you know enough to make the necessary elaborations to what follows.) So for large $n$, \( X_{t+1}|X_t=n \approx \mathcal{N}(n\mu, n\sigma^2) \), regardless of the underlying distribution $p$. When the branching process does not go extinct but grows exponentially, it becomes hard to use the total population size to learn more than the first two moments of the offspring distribution. Because the distribution of \( X_{t+1} \) given \( X_t \) is not exactly Gaussian, some information from $p$ does carry through, especially in the tails. So we do not quite have partial identification in the technical sense, but we do have an interesting, and very real, difficulty when it comes to estimating a key aspect of the model.

permanent link for this note   RSS feed for this note

Notebooks: