Estimating by Minimizing
\[ \newcommand{\Expect}[1]{\mathbb{E}\left[ #1 \right]} \newcommand{\Var}[1]{\mathrm{Var}\left[ #1 \right]} \newcommand{\Expectwrt}[2]{\mathbb{E}_{#2}\left[ #1 \right]} \newcommand{\Varwrt}[2]{\mathrm{Var}_{#2}\left[ #1 \right]} \DeclareMathOperator*{\argmin}{argmin} \]
Attention conservation notice: > 1800 words on basic statistical theory. Full of equations, and even a graph and computer code, yet mathematically sloppy.
The basic ideas underlying asymptotic estimation theory are very simple; most presentations rather cloud the basics, because they include lots of detailed conditions needed to show rigorously that everything works. In the spirit of the world's simplest ergodic theorem, let's talk about estimation.
We have a statistical model, which tells us, for each sample size \( n \), the probability that the observations \( X_1, X_2, \ldots X_n \equiv X_{1:n} \) will take on any particular value \( x_{1:n} \), or the probability density if the observables are continuous. This model contains some unknown parameters, bundled up into a single object \( \theta \), which we need to calculate those probabilities. That is, the model's probabilities are \( m(x_{1:n};\theta) \), not just \( m(x_{1:n}) \). Because this is just baby stats., we'll say that there are only a finite number of unknown parameters, which don't change with \( n \), so \( \theta \in \mathbb{R}^d \). Finally, we have a loss function, which tells us how badly the model's predictions fail to align with the data: \[ \lambda_n(x_{1:n}, m(\cdot ;\theta)) \] For instance, each \( X_i \) might really be a \( (U_i, V_i) \) pair, and we try to predict \( V_i \) from \( U_i \), with loss being mean-weighted-squared error: \[ \lambda_n = \frac{1}{n}\sum_{i=1}^{n}{\frac{{\left( v_i - \Expectwrt{V_i|U_i=u_i}{\theta}\right)}^2}{\Varwrt{V_i|U_i=u_i}{\theta}}} \] (If I don't subscript expectations \( \Expect{\cdot} \) and variances \( \Var{\cdot} \) with \( \theta \), I mean that they should be taken under the true, data-generating distribution, whatever that might be. With the subscript, calculate assuming that the \( m(\cdot; \theta) \) distribution is right.)
Or we might look at the negative mean log likelihood, i.e., the cross-entropy, \[ \lambda_n = -\frac{1}{n}\sum_{i=1}^{n}{\log{m(x_i|x_{1:i-1};\theta)}} \]
Being simple folk, we try to estimate \( \theta \) by minimizing the loss: \[ \widehat{\theta}_n = \argmin_{\theta}{\lambda_n} \]
We would like to know what happens to this estimate as \( n \) grows. To do this, we will make two assumptions, which put us at the mercy of two sets of gods.
The first assumption is about what happens to the loss functions. \( \lambda_n \) depends both on the parameter we plug in and on the data we happen to see. The later is random, so the loss at any one \( \theta \) is really a random quantity, \( \Lambda_n(\theta) = \lambda_n(X_{1:n},\theta) \). Our first assumption is that these random losses tend towards non-random limits: for each \( \theta \), \[ \Lambda_n(\theta) \rightarrow \ell(\theta) \] where \( \ell \) is a deterministic function of \( \theta \) (and nothing else). It doesn't particularly matter to the argument why this is happening, though we might have our suspicions1, just that it is. This is an appeal to the gods of stochastic convergence.
Our second assumption is that we always have a unique interior minimum with a positive-definite Hessian: with probability 1, \[ \begin{eqnarray*} \nabla {\Lambda_n}(\widehat{\theta}_n) & = & 0\\ \nabla \nabla \Lambda_n (\widehat{\theta}_n) & > & 0 \end{eqnarray*} \] (All gradients and other derviatives will be with respect to \( \theta \); the dimensionality of \( x \) is irrelevant.) Moreover, we assume that the limiting loss function \( \ell \) also has a nice, unique interior minimum at some point \( \theta^* \), the minimizer of the limiting, noise-free loss: \[ \begin{eqnarray*} \theta^* & = & \argmin_{\theta}{\ell}\\ \nabla {\ell}(\theta^*) & = & 0\\ \nabla \nabla \ell (\theta^*) & > & 0 \end{eqnarray*} \] Since the Hessians will be important, I will abbreviate \( \nabla \nabla \Lambda_n (\widehat{\theta}_n) \) by \( \mathbf{H}_n \) (notice that it's a random variable), and \( \nabla \nabla \ell (\theta^*) \) by \( \mathbf{j} \) (notice that it's not random).
These assumptions about the minima, and the derivatives at the minima, place us at the mercy of the gods of optimization.
To see that these assumptions are not empty, here's an example. Suppose that our models are Pareto distributions for \( x \geq 1 \), \( m(x;\theta) = (\theta - 1) x^{-\theta} \). Then \( \lambda_n(\theta) = \theta \overline{\log{x}}_n - \log{(\theta - 1)} \), where \( \overline{\log{x}}_n = n^{-1} \sum_{i=1}^{n}{\log{x_i}} \), the sample mean of the log values. From the law of large numbers, \( \ell(\theta) = \theta \Expect{\log{X}} - \log{(\theta-1)} \). To show the convergence, the figure plots \( \lambda_{10} \), \( \lambda_{1000} \) and \( \lambda_{10^5} \) for a particular random sample, and the corresponding \( \ell \). I chose this example in part because the Pareto distribution is heavy tailed, and I actually generated data from a parameter value where the variance of \( X \) is infinite (or undefined, for purists). The objective functions, however, converge just fine.
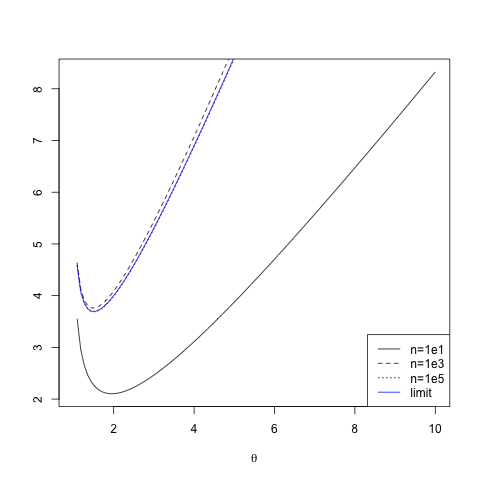
|
| Convergence of objective functions, here, negative average log-likelihoods. (Click on the image for the generating R code.) Note that the limiting, \( n = \infty \) objective function (solid blue line) is extremely close to what we see at \( n = 10^5 \) already. (See here, or more generally here, for pareto.R.) |
With these assumptions made, we use what is about the only mathematical
device employed in statistical theory at this level, which is a Taylor
expansion. Specifically, we expand the gradient \( \nabla \Lambda_n \) around
\( \theta^* \):
\[
\begin{eqnarray*}
\nabla {\Lambda_n}(\widehat{\theta}_n) & = & 0\\
& \approx & \nabla {\Lambda_n}(\theta^*) + \mathbf{H}_n(\widehat{\theta}_n - \theta^*)\\
\widehat{\theta}_n & = & \theta^* - \mathbf{H}_n^{-1}\nabla {\Lambda_n}(\theta^*)
\end{eqnarray*}
\]
The first term on the right hand side, \( \theta^* \), is the
population/ensemble/true minimizer of the loss. If we had \( \ell \) rather
than just \( \Lambda_n \), we'd get that for the location of the minimum. But
since we see \( \ell
\) through
a glass, darkly corrupted by noise, we need to include the extra
term \( - \mathbf{H}_n^{-1}\nabla {\Lambda_n}(\theta^*) \). The Hessian \(
\mathbf{H}_n \) tells us how sharply curved \( \Lambda_n \) is near its
minimum; the bigger this is, the easier, all else being equal, to find the
location of the minimum. The other factor, \( \nabla {\Lambda_n}(\theta^*) \),
indicates how much noise there is — not so much in the function being
minimized, as in its gradient, since after all \( \nabla {\ell}(\theta^*) = 0
\). We would like \( \widehat{\theta}_n \rightarrow \theta^* \), so we have to
convince ourselves that the rest is asymptotically negligible, that \(
\mathbf{H}_n^{-1}\nabla {\Lambda_n}(\theta^*) = o(1) \).
Start with the Hessian. \( \mathbf{H}_n \) is the matrix of second derivatives of a random function: \[ \mathbf{H}_n(\widehat{\theta}_n) = \nabla \nabla \Lambda_n(\widehat{\theta}_n) \] Since \( \Lambda_n \rightarrow \ell \), it would be reasonable to hope that \[ \mathbf{H}_n(\widehat{\theta}_n) \rightarrow \nabla \nabla \ell(\widehat{\theta}_n) = \mathbf{j}(\widehat{\theta}_n) \] We'll assume that everything is nice ("regular") enough to let us "exchange differentiation and limits" in this way. Since \( \mathbf{H}_n(\widehat{\theta}_n) \) is tending to \( \mathbf{j}(\widehat{\theta}_n) \), it follows that \( \mathbf{H}_n = O(1) \), and consequently \( \mathbf{H}_n^{-1} = O(1) \) by continuity. With more words: since \( \Lambda_n \) is tending towards \( \ell \), the curvature of the former is tending towards the curvature of the latter. But this means that the inverse curvature is also stabilizing.
Our hope then has to be the noise-in-the-gradient factor, \( \nabla {\Lambda_n}(\theta^*) \). Remember again that \[ \nabla \ell (\theta^*) = 0 \] and that \( \Lambda_n \rightarrow \ell \). So if, again, we can exchange taking derivatives and taking limits, we do indeed have \[ \nabla {\Lambda_n}(\theta^*) \rightarrow 0 \] and we're done. More precisely, we've established consistency: \[ \widehat{\theta}_n \rightarrow \theta^* \]
Of course it's not enough just to know that an estimate will converge, one also wants to know something about the uncertainty in the estimate. Here things are mostly driven by the fluctuations in the noise-in-the-gradient term. We've said that \( \nabla {\Lambda_n}(\theta^*) = o(1) \); to say anything more about the uncertainty in \( \widehat{\theta}_n \), we need to posit more. It is very common to be able to establish that \( \nabla {\Lambda_n}(\theta^*) = O(1/\sqrt{n}) \), often because \( \Lambda_n \) is some sort of sample- or time- average, as in my examples above, and so an ergodic theorem applies. In that case, because \( \mathbf{H}_n^{-1} = O(1) \), we have \[ \widehat{\theta}_n - \theta^* = O(1/\sqrt{n}) \]
If we can go further, and find \[ \Var{\nabla {\Lambda_n}(\theta^*)} = \mathbf{k}_n \] then we can get a variance for \( \widehat{\theta}_n \), using propagation of error: \[ \begin{eqnarray*} \Var{\widehat{\theta}_n} & = & \Var{\widehat{\theta}_n - \theta^*}\\ & = & \Var{-\mathbf{H}_n^{-1} \nabla {\Lambda_n}(\theta^*)}\\ & \approx & \mathbf{j}^{-1}(\theta^*) \Var{ \nabla {\Lambda_n}(\theta^*)} \mathbf{j}^{-1}(\theta^*)\\ & = & \mathbf{j}^{-1} \mathbf{k}_n \mathbf{j}^{-1} \end{eqnarray*} \] the infamous sandwich covariance matrix. If \( \nabla {\Lambda_n}(\theta^*) = O(1/\sqrt{n} ) \), then we should have \( n \mathbf{k}_n \rightarrow \mathbf{k} \), for a limiting variance \( \mathbf{k} \). Then \( n \Var{\widehat{\theta}_n} \rightarrow \mathbf{j}^{-1} \mathbf{k} \mathbf{j}^{-1} \).
Of course we don't know \( \mathbf{j}(\theta^*) \), because that involves the parameter we're trying to find, but we can estimate it by \( \mathbf{j}(\widehat{\theta}_n) \), or even by \( \mathbf{H}_n^{-1}(\widehat{\theta}_n) \). That still leaves getting an estimate of \( \mathbf{k}_n \). If \( \Lambda_n \) is an average over the \( x_i \), as in my initial examples, then we can often use the variance of the gradients at each data point as an estimate of \( \mathbf{k}_n \). In other circumstances, we might actually have to think.
Finally, if \( \nabla \Lambda_n(\theta^*) \) is asymptotically Gaussian, because it's governed by a central limit theorem, then so is \( \widehat{\theta}_n \), and we can use Gaussians for hypothesis testing, confidence regions, etc.
A case where we can short-circuit a lot of thinking is when the model is correctly specified, so that the data-generating distribution is \( m(\cdot;\theta^*) \), and the loss function is the negative mean log-likelihood. (That is, we are maximizing the likelihood.) Then the negative of the limiting Hessian \( \mathbf{j} \) is the Fisher information. More importantly, under reasonable conditions, one can show that \( \mathbf{j} = \mathbf{k} \), that the variance of the gradient is exactly the limiting negative Hessian. Then the variance of the estimate simplifies to just \( \mathbf{j}^{-1} \). This turns out to actually be the best variance you can hope for, at least with unbiased estimators (the Cramér-Rao inequality). But the bulk of the analysis doesn't depend on the fact that we're estimating by maximum likelihood; it goes the same way for minimizing any well-behaved objective function.
Now, there are a lot of steps here where I am being very loose. (To begin with: In what sense is the random function \( \Lambda_n \) converging on \( \ell \), and does it have to converge everywhere, or just in a neighborhood of \( \theta^* \)?) That is, I am arguing like a physicist. Turning this sketch into a rigorous argument is the burden of good books on asymptotic statistics. But this is the core. It does not require the use of likelihood, or correctly specified models, or independent data, just that the loss function we minimize be converging, in a well-behaved way, to a function which is nicely behaved around its minimum.
Further reading:
- O. E. Barndorff-Nielsen and D. R. Cox, Inference and Asymptotics
- Charles J. Geyer, "Asymptotics of Maximum Likelihood without the LLN or CLT or Sample Size Going to Infinity", arxiv:1206.4762
- Peter J. Huber, "The behavior of maximum likelihood estimates under nonstandard conditions", Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability vol. 1, pp. 221--233 (University of California Press, 1967)
- Aad van der Vaart, Asymptotic Statistics
[1]: "In fact, all epistemologic value of the theory of the probability is based on this: that large-scale random phenomena in their collective action create strict, nonrandom regularity." — B. V. Gnedenko and A. N. Kolmogorov, Limit Distributions for Sums of Independent Random Variables, p. 1. On the other hand, sometimes we can get limits like this as our sensors get better tuned to the signal. ^
Manual trackback: Homoclinic Orbit; The Singing Dodo
Posted at March 18, 2013 00:20 | permanent link