g, a Statistical Myth
Attention conservation notice: About 11,000 words on the triviality of finding that positively correlated variables are all correlated with a linear combination of each other, and why this becomes no more profound when the variables are scores on intelligence tests. Unlikely to change the opinion of anyone who's read enough about the area to have one, but also unlikely to give enough information about the underlying statistical techniques to clarify them to novices. Includes multiple simulations, exasperation, and lots of unwarranted intellectual arrogance on my part.Follows, but is independent of, two earlier posts on the subject of intelligence and its biological basis, and their own sequel on heritability and malleability. This doubtless more than exhausts your interest in reading about the subject; it has certainly exhausted my interest in writing about it.
Disclaimer: A decade ago, some of the senior faculty in my department, i.e., some of the people who will be voting on my contract renewal and tenure, helped put together a book called Intelligence, Genes and Success: Scientists Respond to The Bell Curve. Most, but not all, of the responses in that book were exceedingly negative. I cite some of that work below. Whether this should alter your evaluation of the case I make is for you to decide.Thanks are due to (alphabetically) Carl Bergstrom, Matthew Berryman, John Burke, Mark Liberman, and Aaron Swartz for many helpful suggestions. But, of course, I'm the only one responsible for this, all remaining errors are my own, and it's not in any sense authorized or endorsed by anyone (in particular not by them).
Anyone who wanders into the bleak and monotonous desert of IQ and the nature-vs-nurture dispute eventually gets trapped in the especially arid question of what, if anything, g, the supposed general factor of intelligence, tells us about these matters. By calling g a "statistical myth" before, I made clear my conclusion, but none of my reasoning. This topic being what it is, I hardly expect this will change anyone's mind, but I feel a duty to explain myself.
To summarize what follows below ("shorter sloth", as it were), the case for g rests on a statistical technique, factor analysis, which works solely on correlations between tests. Factor analysis is handy for summarizing data, but can't tell us where the correlations came from; it always says that there is a general factor whenever there are only positive correlations. The appearance of g is a trivial reflection of that correlation structure. A clear example, known since 1916, shows that factor analysis can give the appearance of a general factor when there are actually many thousands of completely independent and equally strong causes at work. Heritability doesn't distinguish these alternatives either. Exploratory factor analysis being no good at discovering causal structure, it provides no support for the reality of g.
These purely methodological points don't, themselves, give reason to doubt the reality and importance of g, but do show that a certain line of argument is invalid and some supposed evidence is irrelevant. Since that's about the only case which anyone does advance for g, however, which accords very poorly with other evidence, from neuroscience and cognitive psychology, about the structure of the mind, it is very hard for me to find any reason to believe in the importance of g, and many to reject it. These are all pretty elementary points, and the persistence of the debates, and in particular the fossilized invocation of ancient statistical methods, is really pretty damn depressing.
Unfortunately, I lack the skill to explain what's going wrong here in a completely non-technical way, other than unsupported assertions of "such-and-such doesn't work". Rather than just pontificate, I will try to explain, but presume that you know what things like variance and correlation are, and what a correlation matrix is, or at least that you used to.
The origin of g: Spearman's original general factor theory
Scores on intelligence tests are correlated with each other; people who do better than average on one test tend to do better than average on another. The same is true of school grades and many other measures of human performance. The idea that these correlations are due to a single "general factor of intelligence", what has come to be called g, originated with Charles Spearman at the turn of the 20th century. Spearman's idea was that a student's grade in, say, English was the sum of two factors, a general factor, common to all subjects, and a specific factor unique to English, plus random, noisy, test-to-test variability. Similarly grades in math would be the sum of the general factor, a math-specific factor, and noise. The specific factors were, Spearman thought, completely uncorrelated, so all the correlations between math and English grades would be due to the general factor. This implied that the partial correlations among test scores — the residual correlation left after controlling for the common factor — should be zero, which, in Spearman's original data, they were, or near enough. [1] Even though g was not directly observable [2], these vanishing partial correlations gave Spearman considerable confidence in his theory, and launched it upon the world.
Spearman's political views were, by my lights, both abhorrent and stupid [3], but so what? (Fisher wasn't much better, but I'm not about to give up maximum likelihood, or even write off The Genetical Theory of Natural Selection.) The two-factor theory was a genuinely scientific theory of considerable scope and empirical content, which would have been very important if it was true. The way we can unambiguously tell that it had falsifiable empirical content is that it was, in fact, falsified. Looking at larger and more diverse data sets, it became clear that the partial correlations among scores on mental ability tests were not zero, or even close enough to attribute the difference to chance. Put to reasonably severe tests, it failed. I don't think there is anyone left who still seriously argues for Spearman's g in this sense.
The modern g
Since Spearman's theory of g is about as refuted as a statistical hypothesis gets, why does g still feature in arguments about social policy and education? Isn't this as though some parties in the global warming debate had climate models involving phlogiston and caloric? The answer is that psychometricians responded to the difficulties of the one-general-factor theory by developing models with multiple unobserved factors. (The leading name here is that of Thurstone, whose classic paper "The Vectors of Mind" is definitely worth reading.) The bulk of the correlations between tests get attributed to a leading common factor, still called g. The smaller but non-negligble correlations left after accounting for this g are attributed to other, lesser factors. The reality and importance of g is held to follow from the fact that it accounts for so much of the correlations among the tests. A still later, and still subtler, strategy is that of hierarchical factor analysis: find multiple factors from the correlations among test scores, and then recursively find higher-order factors from the correlations among the lower-order factors, until finally only a single factor remains, which is declared to be g. (For an exposition of this last approach by one of its most prominent advocates, see John Carroll's contribution to Intelligence, Genes, and Success.)
These may sound like ad hoc face-saving maneuvers, but you could also argue that they're' reasonable extensions of theory, keeping the working bits and fixing some broken ones. (After all, an important part of the mechanical theory of heat is explaining why heat does, in many ways, act like a subtle fluid.) The trouble is that, in turning factor analysis into a better tool for describing correlations, Thurstone et al. made it into a next-to-useless tool for explaining correlations, and most users of the tool then and since have never really grasped the problem. Since this is very important to what follows, I want to take some time to explain the differences between "exploratory" and "confirmatory" factor analyses, and why using the former to find causal structure is telling time with a stopped clock. No part of my argument is at all original; it's old news to people who actually study psychometric methods and causal inference in general. In fact, even, or especially, if you think that what I'm saying is weak-minded politically correct rubbish and I really ought to know better, I strongly urge you to read the linked papers by Borsboom (with the discussion) and by Glymour.
Exploratory factor analysis vs. causal inference
Exploratory factor analysis is a useful piece of descriptive statistics, and as such I expound and endorse it quite happily when I teach data mining. [4] The basic idea, as we saw with Spearman's theory, is to take a large number of correlated measurements, and to represent them as linear combinations of a smaller number of "factors" which are common to all or many of the measurements, plus idiosyncratic noise terms. The trick with exploratory factor analysis is that the factors are, themselves, linear combinations of the observed measurements, and all the methods for factor analysis are ways of searching for combinations which correlate well with the observations. There are various criteria you can use to do this, which all tend to give similar-but-not-identical results in practice. [5]
This is a perfectly reasonable and useful way to do data reduction and exploratory pattern hunting. One of the examples in my data-mining class is to take a ten-dimensional data set about the attributes of different models of cars, and boil it down to two factors which, together, describe 83 percent of the variance across automobiles. [6] The leading factor, the automotive equivalent of g, is positively correlated with everything (price, engine size, passengers, length, wheelbase, weight, width, horsepower, turning radius) except gas mileage. It basically says whether the car is bigger or smaller than average. The second factor, which I picked to be uncorrelated with the first, is most positively correlated with price and horsepower, and negatively with the number of passengers — the sports-car/mini-van axis.
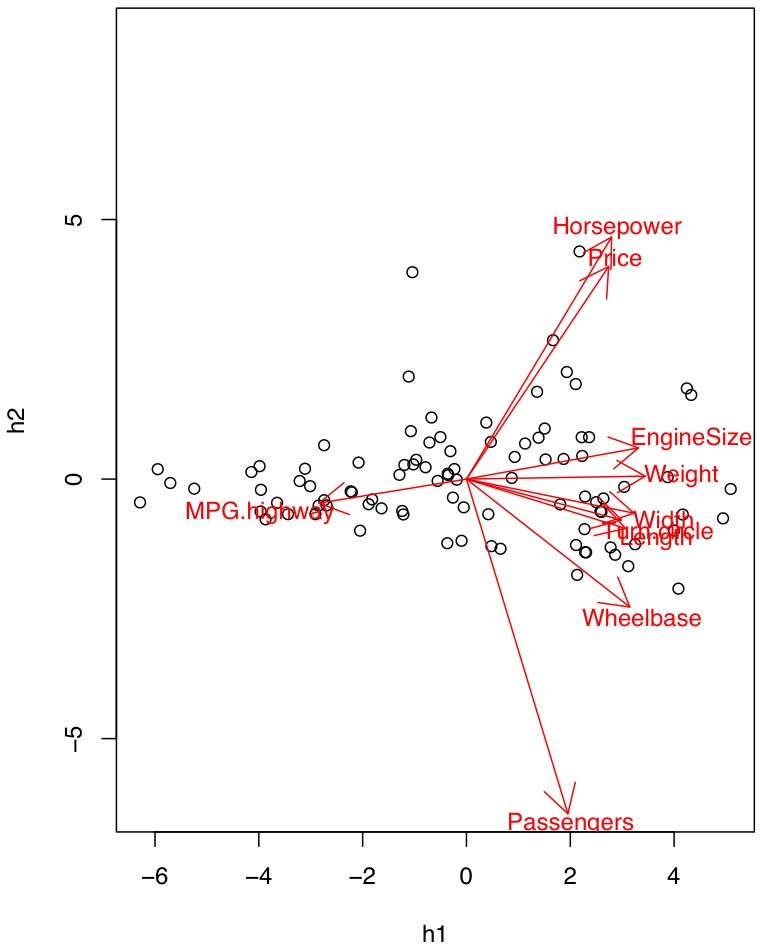 |  |
| Left: Relations between the first two principal components and the measured variables. Right: The individual cars plotted against the principal components. Click for full-size PDFs. | |
In this case, the analysis makes up some variables which aren't too implausible-sounding, given our background knowledge. Mathematically, however, the first factor is just a weighted sum of the traits, with big positive weights on most variables and a negative weight on gas mileage. That we can make verbal sense of it is, to use a technical term, pure gravy. Really it's all just about redescribing the data.
This brings me to the other major sort of factor analysis, what's called "confirmatory" factor analysis. This is about checking a model where some latent, unobserved variables are supposed to account for the relations among the actual observations. To simplify, the logic is that if the model is right, then we should get certain patterns of correlations and no others — like checking whether the partial correlations are zero, as Spearman's original model required them to be, but adapted to other latent structures. This is a genuinely inferential and not just descriptive piece of statistics. It's also a pretty modest one, since failing one of these tests is decisive, but passing often isn't very informative, because, as we'll see, radically different arrangements of latent factors can give basically the same pattern of observed correlations. (In the jargon, the power of these tests can be very low at reasonable sample sizes.) It is very striking how infrequently one finds people who use exploratory factor analysis checking things with confirmatory factor analysis, for which I think a lot of blame must rest with teachers of statistics, myself included. If my two-factor model for the cars was right, then all of the correlation between (say) gas mileage and horsepower should be due to their respective correlations with the two factors, with no partial correlation between them once the factors are accounted for. The data falsify this hypothesis at any reasonable level of significance. I do not, however, teach my students to do this: mea culpa.
(And it's not just me. One of the most prominent ideas put forward on the basis of these exploratory techniques, aside from the general intelligence factor, is what's called the five factor theory of personality traits. This quite robustly fails confirmatory factor analyses: the "Big Five", despite being made up for the purpose, don't actually fit the correlations in the data, even on personality tests designed using the theory. This has done next to nothing to make personality psychologists rethink, revise, or discard the theory, and leads mild-mannered psychometricians to tear their hair in frustration.)
So: exploratory factor analysis exploits correlations to summarize data, and confirmatory factor analysis — stuff like testing that the right partial correlations vanish — is a prudent way of checking whether a model with latent variables could possibly be right. What the modern g-mongers do, however, is try to use exploratory factor analysis to uncover hidden causal structures. I am very, very interested in the latter pursuit, and if factor analysis was a solution I would embrace it gladly. But if factor analysis was a solution, when my students asked me (as they inevitably do) "so, how do we know how many factors we need?", I would be able to do more than point them to rules of thumb based on squinting at "scree plots" like this and guessing where the slope begins. (There are ways of estimating the intrinsic dimension of noisily-sampled manifolds, but that's not at all the same.) More broadly, factor analysis is part of a larger circle of ideas which all more or less boil down to some combination of least squares, linear regression and singular value decomposition, which are used in the overwhelming majority of work in quantitative social science, including, very much, work which tries to draw causal inferences without the benefit of experiments. A natural question — but one almost never asked by users of these tools — is whether they are reliable instruments of causal inference. The answer, unequivocally, is "no".
I will push extra hard, once again, Clark Glymour's paper on The Bell Curve, which patiently explains why these tools are just not up to the job of causal inference. (Maybe more than two people will follow that link this time.) They do not, of course, become reliable when used by the righteous, and Glymour was issuing such warnings long before Herrnstein and Murray's book appeared to trouble our counsels. The conclusions people reach with such methods may be right and may be wrong, but you basically can't tell which from their reports, because their methods are unreliable.
This is why I said that using factor analysis to find causal structure is like telling time with a stopped clock. It is, occasionally, right. Maybe the clock stopped at 12, and looking at its face inspires you to look at the sun and see that it's near its zenith, and look at shadows and see that they're short, and confirm that it's near noon. Maybe you'd not have thought to do those things otherwise; but the clock gives no evidence that it's near noon, and becomes no more reliable when it's too cloudy for you to look at the sun.
Now, I could go over the statistical issues involved in reliable causal inference, and why factor analysis doesn't measure up. But if I've learned anything teaching it's that examples are vastly more effective than proofs. (If you really want to know, start with Pearl and Spirtes, Glymour and Scheines.) So I'm going to show you some cases where you can see that the data don't have a single dominant cause, because I made them up randomly, but they nonetheless give that appearance when viewed through the lens of factor analysis. I learned this argument from a colleague, but so that they can lead a quiet life I'll leave them out of this; versions of the argument date back to Godfrey Thomson in the 1910s [7].
Correlations explain g, not the other way around
If I take any group of variables which are positively correlated, there will, as a matter of algebraic necessity, be a single dominant general factor, which describes more of the variance than any other, and all of them will be "positively loaded" on this factor, i.e., positively correlated with it. Similarly, if you do hierarchical factor analysis, you will always be able to find a single higher-order factor which loads positively onto the lower-order factors and, through them, the actual observables [8] What psychologists sometimes call the "positive manifold" condition is enough, in and of itself, to guarantee that there will appear to be a general factor. Since intelligence tests are made to correlate with each other, it follows trivially that there must appear to be a general factor of intelligence. This is true whether or not there really is a single variable which explains test scores or not.
It is not an automatic consequence of the algebra that the apparent general factor describes a lot of the variance in the scores. Nonetheless, while less trivial, it is still trivial. Recall that factor analysis works only with the correlations among the measured variables. If I take an arbitrary set of positive correlations, provided there are not too many variables and the individual correlations are not too weak, then the apparent general factor will, typically, seem to describe a large chunk of the variance in the individual scores.
To support that statement, I want to show you some evidence from what happens with random, artificial patterns of correlation, where we know where the data came from (my computer), and can repeat the experiment many times to see what is, indeed, typical. So that you don't have to just take my word for this, I describe my procedure, and link to my simulation code, in a footnote [9].
Here is the first correlation matrix R produced for me after I debugged my code, for five variables:
1.000 0.399 0.683 0.774 0.241 0.399 1.000 0.403 0.251 0.002 0.683 0.403 1.000 0.823 0.336 0.774 0.251 0.823 1.000 0.665 0.241 0.002 0.336 0.665 1.000
The way to read this is that the number at the intersection of row number I and column number J is the correlation between variable number I and variable number J. All of the entries on the diagonal are 1, because everything is perfectly correlated with itself. Some of these variables are strongly correlated (e.g., the third and fourth, 0.823), while others are not (e.g., the second and fifth, 0.002). All of them, however, are positively correlated. If these variables represented actual observations, this pattern of correlations would rule out the possibility of some causal structures underlying the measurements, but would still be compatible with a huge range of different mechanisms. But remember, this is a completely random example, with no real causal factors behind it whatsoever.
At this stage, I could have done a factor analysis of the correlation matrix, but to make things look more realistic, I instead generated "test scores" for 1000 "subjects" with these correlations, with each test having a mean of 100 and a standard deviation of 15 (just like an IQ test). I then used a completely standard piece of software (R's factanal function; a maximum-likelihood routine) to find the single factor which best accounted for the correlations in the measurements.
| variable | 1 | 2 | 3 | 4 | 5 |
| loading | 0.782 | 0.279 | 0.814 | 0.998 | 0.668 |
This one factor would describe more than half (0.559) of the variance in the results, which is really quite respectable by many social-science standards. For example, a typical value for the fraction of variance described by g on actual intelligence tests seems to be somewhere in the range of a quarter to two-thirds, and generally in the lower part of that range, say around a third.
From looking at the table of loadings, it appears that variable #2, whatever it is, is not well-described by the factor. If I think of the factor as something real — intelligence or athleticism or neuroticism or car-bigness, it doesn't matter — I might then drop variable #2 from my battery of tests. If I do so and re-calculate the factor loadings, they hardly change,
| variable | 1 | 3 | 4 | 5 |
| loading | 0.782 | 0.814 | 0.998 | 0.669 |
and now the single factor accounts for more than two thirds (0.679) of the variance. I will come back to this point later.
These results are no fluke. [10] Repeating this a thousand times, each with a different randomly-generated correlation matrix, the mean proportion of variance described by a single factor is 0.471, with a standard deviation of 0.079. (So my first random sample was a little on the high side, but not remarkably so.) If I repeat the experiment with six imaginary tests rather than five, then the mean proportion of variance described is 0.432, with a standard deviation of 0.065. If I stick to five dimensions, and let the correlations go over the whole range from -1 to 1, then I get a somewhat smaller mean proportion-of-variance-described, namely 0.400, with nearly the same standard deviation (0.070). If, on the other hand, I confine myself to correlations in the range from 0 to 1/2, then I get a much smaller mean (0.289±0.041), but still one many people would be able to publish proudly. If I force the correlation coefficients to all be negative, in the range -1 to 0, again it's smaller but not negligible (0.294±0.029). And so on, and so on.
Why does this matter? Well, if you take people and give them pretty much any battery of tests of mental abilities, skills and knowledge you care to name, you will find positive correlations among the scores — especially if you exclude people who have received specialized training in skills relevant to one test or another, or the tests on which people have been trained. [11] In this situation, all that seeing a lot of variance described by the leading factor tells you is that, in fact, there are lots of positive correlations. This is what Thomson was pointing out, all those years ago, when he said that the apparent descriptive strength of the leading factor for test results was more a mathematical theorem than a psychological fact.
How to make 2766 independent abilities look like one g factor
But — and I can hear people preparing this answer already — doesn't the fact that there are these correlations in test scores mean that there must be a single common factor somewhere? To which question a definite and unambiguous answer can be given: No. You can get strong positive correlations — even ones with vanishing partial correlations, so it looks like there's one factor — even when all the real causes are about equal in importance and completely independent of one another. This was, again, first demonstrated by Thomson — in 1914. I'll go over a slight variant of his original model, in the hope that it will lessen the odds that we have to spend the next 93 years debating what ought to be a closed issue.
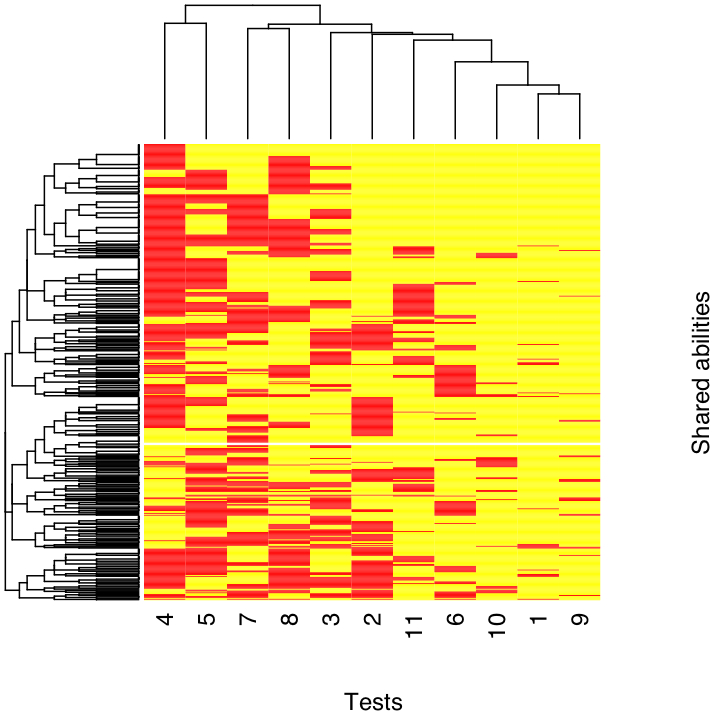
The model goes like this: there are lots of different mental abilities, a huge number of them. (Thomson sometimes called them "factors", but I'll reserve that for the things found by factor analysis.) Any one given intelligence test calls on many of these abilities, some of which are shared with other tests, some of which are specific to that test (at least among those being analyzed). For each test, draw a number between 1 and 500; that is the number of shared abilities used in that test. Draw another number between 1 and 500; that is the number of test-specific abilities it uses. In my simulation, I used 11 tests, because one of the more widely used IQ measures, the revised Weschler Adult Intelligence Scale, was a battery of 11 tests. (The latest incarnation, the WAIS-III, has 14 tests, but the results would be the same.) So here's what I got:
| variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| shared abilities | 478 | 326 | 313 | 154 | 229 | 405 | 266 | 278 | 479 | 462 | 378 |
| specific abilities | 28 | 62 | 45 | 78 | 473 | 26 | 195 | 473 | 403 | 150 | 333 |
| total | 506 | 388 | 358 | 232 | 702 | 431 | 461 | 751 | 882 | 612 | 711 |
To determine which shared abilities go with which variable, I draw a sample of the specified size from my pool of 500 abilities. Now variable 1 (for example) is determined by 506 abilities, 478 of which it might have in common with other tests, and I know which abilities those 478 are. The total number of abilities invoked in this model is 2766. To make the result which is coming as stark as possible, Thomson assumed, as I will, that there is no dependence whatsoever among these abilities; they are totally and completely uncorrelated. For convenience, I'll assume that these abilities are not only independent but also identically distributed (IID); to keep things looking familiar, I made them normally distributed with a mean of 100 and a standard deviation of 15. Some abilities are involved in more than one test, but since there are 3 which are shared by all the tests, and 34 which are shared by at least ten of them, it's hard to say that there is a common ability. (Also, every shared ability is shared by at least three tests.) Since every test involves at least 232 distinct abilities, these widely-shared abilities are not overwhelming determinants of the test scores, either.
To generate test scores, I made up a random sample of 1000 independent individuals, and assigned them values of these 2766 abilities. I then summed the abilities, as prescribed, to get scores on the 11 tests. To add an air of verisimilitude, I topped each test score off with a little extra noise (mean zero, s.d. 15), so that if I re-tested my "subjects", I wouldn't get exactly the same results, but the tests would be highly reliable by the usual measures. Once again, let me emphasize that every ability contributing to the test scores is completely independent of every other, and none of them is preponderant on any of the tests, much less all of them.
When I do a factor analysis as before, I find that a single made-up factor, call it g, describes nearly half (0.478) of the standardized variance. The g loadings are as follows:
| variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| loadings | 0.955 | 0.756 | 0.758 | 0.465 | 0.416 | 0.859 | 0.539 | 0.431 | 0.708 | 0.829 | 0.634 |
Even the smallest of these would be pretty respectable, and some of them are great; you can compare them to the factor loadings for some data from the children's version of the Weschler scale obtained here by an advocate of g. The correlation between my variables' factor loadings and the number of shared abilities they draw on is +0.816. (As they used to say: This is no coincidence, comrades!) More, if I do a standard test for whether this pattern of correlations is adequately explained by a single factor, the data pass with flying colors (chi-squared is 38.41 on 44 degrees of freedom, p-value of 0.709). All of which is, by construction, a complete artifact.
Once again, this isn't a fluke. Repeating the simulation from scratch (i.e., coming up with completely new mappings between abilities and tests each time) a thousand times, I get an mean descriptive strength for the g factor of 0.290±0.066 — so, again, my initial trial was on the high side, but, honest, it was the first trial after I got the bugs out. You can use my code for this simulation to play around with what happens as you vary the number of tests and the number of abilities.
Now, I don't mean to suggest this model of thousands of IID abilities adding up as a serious depiction of how thought works, or even of how intelligence test scores work. My point, like Thomson's, is to show you that the signs which the g-mongers point to as evidence for its reality, for there having to be a single predominant common cause, actually indicate nothing of the kind. Thomson's model does this in a particularly extreme way, where those signs are generated entirely through the imprecision of our measurements. There are other models — for instance, the "dynamical mutualism" model of van der Maas et al. ("A Dynamical Model of General Intelligence: The Positive Manifold of Intelligence by Mutualism", Psychological Review 113 (2004): 842--861) which produce those signs from interacting processes, with nothing resembling a general factor in their causal structure. (This should surprise no one who's even casually familiar with distributed systems or self-organization.) Those supposed signs of a real general factor are thus completely uninformative as to the causes of performance on intelligence tests.
Heritability is irrelevant
Someone will object that g is highly heritable, and say that this couldn't be true if it wasn't just an artifact. But this also has no force: Thomson's model can easily be extended to give the appearance of heritability, too.
Having spent far too long, in a previous post, covering what heritability is, why estimating the heritability of IQ is difficult to meaningless, and why it tells us nothing about how malleable IQ is, I won't re-traverse that ground here. Determining the heritability of an unobserved variable like g raises a whole extra set of problems — there is a reason you see so many more estimates of the heritability of IQ than of g — though if you want to define "general intelligence" as a certain weighted sum of test scores, that is at least operationally measurable. Suppose that, mirabile dictu, all the problems are solved and we learn the heritability of g, and it's about the same as the best estimate of the narrow-sense heritability of IQ, which is 0.34. Does it make sense to go from "g is heritable" to "g is real and important"?
I have to say that I find it an extraordinarily silly inference, and I'm astonished that anyone who understands how to calculate a heritability has ever thought otherwise. Height, in developed countries, has a heritability around 0.8. Blood triglyceride levels have a heritability of about 0.5. Thus the sum of height and triglycerides is heritable. How heritable will depend on the correlations between the additive components of height and those of triglycerides; assuming, for simplicity, that there aren't any, the heritability of their sum will be anywhere from 0.8 and 0.5, depending on the units we measure each variable in. The fact that this trait is heritable doesn't make it any less meaningless.
It'd still be embarrassing for the Thomson model if it couldn't produce its appearance, since after all no one is saying that the measured (or even real) heritability of IQ is always and exactly zero. But that's very easy, and the logic is the same as for combining height and triglycerides. Assume, as in classical biometric models, that the strength of each ability for each person is then the sum of three components, one purely genetic and additive across genes, one purely genetic and associated with gene interactions, and one purely environmental, and that these are perfectly independent of each other. Say that the strict-sense heritability of each ability, the ratio of the additive genetic variance to the total variance in the ability, is 0.5. The test scores, being linear combinations of abilities plus noise, will also be heritable. The g found by factor analysis, being a linear combination of the test scores, is itself a linear combination of the abilities and noise, and so, in turn, heritable. [12]
How heritable g would look would depend on whether the environmental contributions to the different abilities were correlated. If they are uncorrelated, then the heritability of the test scores will be slightly less than 0.5 (less, because of the extra measurement noise). If the environmental contributions to different abilities are positively correlated, the total environmental variance in the test scores will be larger, so their heritability will be lower. Since, to repeat, the meta-analysis of Devlin, Daniels and Roeder puts the heritability of IQ at around 0.34, that's fine.
In a sentence: Thomson's ability-sampling model not only creates the illusion of a general factor of intelligence where none exists, it can also make this illusory factor look heritable.
What has the factorial analysis of human abilities ever done for us?
It might be the case that, while exploratory factor analysis isn't a generally reliable tool for causal inference, for some reason it happens to work in psychological testing. To believe this, I would want to see many cases where it had at least contributed to important discoveries about mental structure which had some other grounds of support. These are scarce. The five-factor theory of personality, as I mentioned above, is probably the best candidate, and it fails confirmatory factory analysis tests. As Clark Glymour points out, lesion studies in neuropsychology have uncovered a huge array of correlations among cognitive abilities, many of them very specific, none of which factor analyses predicted, or even hinted at. Similarly, congenital defects of cognition, like Williams's Syndrome, drive home the point that thought is a biological process with a genetic basis (if that needs driving). But Williams's Syndrome is simply not the kind of thing anyone would have expected from factor analysis, and for that matter a place where the IQ score, while not worthless, is not much help in understanding what's going on.
Stepping back a bit, the lack of success of factor analysis in psychology is actually surprising, because of the circularity in how psychological tests have come to be designed. The psychologists start with some traits or phenomena, which seem somehow similar to them, to exhibit a common quality, be it "intelligence" or "neuroticism" or "authoritarianism" or what-have-you. The psychologists make up some tests where a high score seems, to intuition, to go with a high degree of the quality. They will even draw up several such tests, and show that they are all correlated, and extract a common factor from those correlations. So far, so good; or at least, so far, so non-circular. This test or battery of tests might be good for something. But now new tests are validated by showing that they are highly correlated with the common factor, and the validity of g is confirmed by pointing to how well intelligence tests correlate with one another and how much of the inter-test correlations g accounts for. (That is, to the extent construct validity is worried about at all, which, as Borsboom explains, is not as much as it should be. There are better ideas about validity, but they drive us back to problems of causal inference.) By this point, I'd guess it's impossible for something to become accepted as an "intelligence test" if it doesn't correlate well with the Weschler and its kin, no matter how much intelligence, in the ordinary sense, it requires, but, as we saw with the first simulated factor analysis example, that makes it inevitable that the leading factor fits well. [13] This is circular and self-confirming, and the real surprise is that it doesn't work better.
I don't want to be mis-understood as being on some positivist-behaviorist crusade against inferences to latent mental variables or structures. As I said, my deepest research interest is, exactly, how to reconstruct hidden causal structures from data. Furthermore, I think it's pretty plain that psychologists have found compelling evidence for many kinds of latent mental structure. For instance, I defy anyone to explain the experimental results on mental rotation without positing mental representations which act in very specific ways. But exploratory factor analysis is not a solution to this problem.
Doing without g
The end result of the self-confirming circle of test construction is a peculiar beast. To the extent g correlates with anything from actual cognitive psychology, it's working memory capacity (see this, and especially the conclusion). If we want to understand the mechanisms of intelligent thought, how they are implemented biologically, and how they grow and flourish or fail to do so, I cannot see how this helps at all.
Of course, if g was the only way of accounting for the phenomena observed in psychological tests, then, despite all these problems, it would have some claim on us. But of course it isn't. My playing around with Thomson's ability-sampling model has taken, all told, about a day, and gotten me at least into back-of-the-envelope, Fermi-problem range. In fact, the biggest problem with Thomson's model is that the appearance of g is too strong, since it easily passes tests for there being only a single factor, when real intelligence tests, such as the Weschler, all fail them. If it wasn't a distraction from my real work, I'd look into whether weakening the assumption that tests are completely independent, uniform samples from the pool of shared abilities couldn't produce something more realistic. (In particular, I'd try self-reinforcing urn schemes.) If we must argue about the mind in terms of early-twentieth-century psychometric models, I'd suggest that Thomson's is a lot closer than the factor-analytical ones to what's suggested by the evidence from cognitive psychology, neuropsychology, functional brain imaging, general evolutionary considerations and, yes, evolutionary psychology (which I think well of, when it's done right): that there are lots of mental modules, which are highly specialized in their information-processing, and that almost any meaningful task calls on many of them, their pattern of interaction shifting from task to task. [14] There is, of course, no need to limit ourselves to early 20th century psychometrics.
All of this, of course, is completely compatible with IQ having some ability, when plugged into a linear regression, to predict things like college grades or salaries or the odds of being arrested by age 30. (This predictive ability is vastly less than many people would lead you to believe [cf.], but I'm happy to give them that point for the sake of argument.) This would still be true if I introduced a broader mens sana in corpore sano score, which combined IQ tests, physical fitness tests, and (to really return to the classical roots of Western civilization) rated hot-or-not sexiness. Indeed, since all these things predict success in life (of one form or another), and are all more or less positively correlated, I would guess that MSICS scores would do an even better job than IQ scores. I could even attribute them all to a single factor, a (for arete), and start treating it as a real causal variable. By that point, however, I'd be doing something so obviously dumb that I'd be accused of unfair parody and arguing against caricatures and straw-men.
If, after looking at your watch, you say that it's 12 o'clock, and I point out that your watch has stopped at 12, I am not saying that it's not 12 o'clock, just that your watch doesn't actually give you any evidence about the time. Similarly, pointing out that factor analysis and related techniques are unreliable guides to causal structure does not establish the non-existence of a one-dimensional latent variable driving the success of almost all human mental performance. It's possible that there is such a thing. But the major supposed evidence for it is irrelevant, and it accords very badly with what we actually know about the functioning of the brain and the mind.
The refrigerator-mother of methodology
I am not sure what the oddest aspect of this situation is, because there are so many. It may be a statistician's bias, but the things I keep dwelling on are the failures of methodology, which are not, alas, confined to all-correlations-all-the-time psychologists, but also seen in the right (that is, wrong) sort of labor-market sociologist, economists who regress countries' growth rates on government policies, etc., etc. As the late sociologist Aage Sorensen said (e.g. here), the sort of social science which tries to identify causal effects by calculating regression coefficients or factor loadings stops where the scientist's work ought, properly, to begin. (A more charitable view would be that these researchers are piling up descriptions, and hoping that someone will come along, any decade now, with explanations.) Many psychometric and econometric theorists know much better, but they seem to have little influence on practice. To paraphrase Hume:
When we run over libraries, persuaded of these principles, what havoc must we make? If we take in our hand any paper; of macroeconomics or correlational psychology, for instance; let us ask, Does it draw its causal inferences from observations with consistent methods? No. Does it draw its causal inferences from experiments, controlled or randomized? No. Commit it then to the recycling bin: for it can contain nothing but sophistry and illusion.
If I want quick summaries of my data, then means, variances and correlations are reasonable things to use, especially if all the distributions are close to Gaussian. If I want to do serious analyses, I need to start comparing distributions, and it's not as if there aren't methods to do this. If I want to do data mining, then sticking to easily-manipulated linear models makes lots of sense; if I want to find causal relationships, at the very least I should test for nonlinearities (which hardly anyone ever seems to do in the IQ field), or, better yet, turn to non-parametric estimates. If there are lots of positive correlations and I want to summarize them, then finding some factors and checking them by decomposing the variance is one reasonable trick. If I want to argue that there must be a preponderant common cause, it's no good to keep pointing out how much of the variance that first factor describes, when plenty of other, incompatible causal structures will give me that too. (There is a name for this mode of reasoning.) An intelligent response to this criticism would be to look for other aspects of the data (including things other than correlation coefficients), or maybe even new experiments, which could tell apart different causal structures. The fact that, 103 years after Spearman, everyone is still just manipulating the correlation matrix shows the lack of such intelligence.
I have deliberately tried to avoid, here, the issues which make the argument about g and IQ so much more heated than ones about, say, labor-market sociology. But those issues do exist, and are heated, and so you might think that they might drive people to use better methods which could help settle the questions. This doesn't seem to happen. Some examples:
- If you insist on looking at differences in IQ scores between social groups, and doing so without trying real causal inference, it is still mystifying to me why you would, at this late date, stick to comparing means, variances and correlations. It would be vastly more informative to look at the whole relative distribution. This, in turn, can be adjusted for the relative distribution of covariates, in much more flexible and powerful ways than ordinary regression allows. The math should not be beyond anyone who understands what a distribution function is.
- The propensity-score-matching method of estimating causal effects, due to Don Rubin and co-workers, can be adapted to the meanest understanding, but I can't find anyone who's done the obvious study of using it to estimate the difference in IQ between blacks and whites of similar education, health, economic status, etc. (If you know of such a study, tell me.) This would in no way tell us whether the gap (if there really is one) was genetic, but it would tell us how big a mean difference we're looking at, in a way which regression simply can't.
- Taking the IQ gap at face value, a persistent question has been whether the tests are biased. Suppose there is an underlying variable of general intelligence. (I doubt it, but I've been wrong before.) Nobody claims that IQ tests perfectly measure general intelligence. So we have a latent trait, and an imperfect index of the trait which shows a difference between groups. The question is whether the index measures the trait the same way in the two groups. What people have gone to great lengths to establish is that IQ predicts other variables the same way for the two groups, i.e., that when you plug it into regressions you get the same coefficients. This is not the same thing, but it does have a bearing on the question of measurement bias: it provides strong reason to think it exists. As Roger Millsap and co-authors have shown in a series of papers going back to the early 1990s (e.g. this one from 1997, or this early treatment of the non-parametric case), if there really is a difference on the unobserved trait between groups, and the test has no measurement bias, then the predictive regression coefficients should, generally, be different. [15] Despite the argument being demonstrably wrong, however, people keep pointing to the lack of predictive bias as a sign that the tests have no measurement bias. (This is just one of the demonstrable errors in the 1996 APA report on intelligence occasioned by The Bell Curve.)
- Since there's been persistent doubt about whether intelligence tests measure intrinsic ability or acquired knowledge, I'd have hoped that someone would do the experiment of controlling what the test-takers know. Nobody seems to have tried this until very recently, and lo and behold it makes the black-white IQ gap go away, and this on tests which are quite respectably g-loaded, i.e., correlated with all the other tests [16].
The psychologist Robert Abelson has a very nice book on Statistics as Principled Argument where he writes that "Criticism is the mother of methodology". I was going to say that such episodes cast that in doubt, but it occurred to me that Abelson never says what kind of mother. To combine Abelson's metaphor with Harlow's famous experiments on love in monkeys, observational social science has been offered a choice between two methodological mothers, one of the warm and cuddly and familiar and utterly un-nourishing (the old world of linear regression, analysis of variance, factor analysis, etc.), the other cold, metallic, hurtful and actually able to help materially (statistical methods which are at least not definitely unable to do what people want). Not surprisingly, social scientists, being primates, overwhelmingly go for the warm fuzzies. This, to me, indicates a deep failure on the part of the statistical profession to which I am otherwise proud to belong. It is never a good sign when your discipline's knowledge is the wire-mesh mother all the baby monkeys avoid if at all possible. Less metaphorically, the perpetuation of these fallacies decade after decade shows there is something deeply amiss with the statistical education of social scientists.
Summary
Building factors from correlations is fine as data reduction, but deeply unsuited to finding causal structures. The mythical aspect of g isn't that it can be defined, or, having been defined, that it describes a lot of the correlations on intelligence tests; the myth is that this tells us anything more than that those tests are positively correlated. It has been known for almost as long as factor analysis has been around that positive correlations can arise in many ways which involve nothing remotely like a general factor of intelligence. Thomson's ability-sampling model, with its myriad independent causes rather than a single general cause, is the oldest and most extreme counter-example, but it is far from the only one. It is still conceivable that those positive correlations are all caused by a general factor of intelligence, but we ought to be long since past the point where supporters of that view were advancing arguments on the basis of evidence other than those correlations. So far as I can tell, however, nobody has presented a case for g apart from thoroughly invalid arguments from factor analysis; that is, the myth.
In primitive societies, or so Malinowski taught, myths serve as the legitimating charters of practices and institutions. Just so here: the myth of g legitimates a vast enterprise of intelligence testing and theorizing. There should be no dispute that, when we lack specialized and valid instruments, general IQ tests can be better than nothing. Claims that they are anything more than such stop-gaps — that they are triumphs of psychological science, illuminating the workings of the mind; keys to the fates of individuals and peoples; sources of harsh truths which only a courageous few have the strength to bear; etc., etc., — such claims are at present entirely unjustified, though not, perhaps, unmotivated. They are supported only by the myth, and acceptance of the myth itself rests on what I can only call an astonishing methodological backwardness.
The bottom line is: The sooner we stop paying attention to g, the sooner we can devote our energies to understanding the mind.
[1]: To be pedantic, Spearman didn't see that partial correlation coefficients were nearly zero, because I think partial correlations weren't invented yet. Instead he saw that certain "tetrad" equations involving the total correlations held, nearly; satisfying those equations is equivalent to the partial correlations vanishing.
[2]: It's worth noting a subtle point here: even if the two-factor theory is true, g cannot, under any circumstances, be calculated directly from observed test scores, so the idea that it gives us an operational and objective definition of general intelligence is, in a word, wrong.
Remember that each test score is supposed to be the sum of g, a test-specific factor, and a little bit of noise. If we repeated the tests many times on the same person and averaged the results, the noise terms would start to cancel each other out. Suppose we could even repeat the tests infinitely often, so that the noise went away completely. If we had k different tests, we would still be left with k equations, one for each test, and k+1 unknowns, those being the k specific factors and the one general factor. Such an underdetermined system of equations has no unique solution. (Unless, that is, one of the tests measures the general factor alone, or two of the tests have exactly the same "specific" factor, in which case there are only k unknowns.) This "underdetermination" appears to have been first pointed out by E. B. Wilson in Science in 1928, and has, unsurprisingly, never been resolved. Statistically speaking, the model is over-parameterized and so non-identifiable, because different combinations of the factors give exactly the same distribution of results. Scoring above average on all the tests, e.g., might be due to (i) an above-average general factor and average specific factors, (ii) an average general factor and above-average specific factors, (iii) really-above-average specific factors and a way-below-average general factor, etc. (More combinations arise if someone scores above average on some but not all tests.) Assuming a certain prior distribution for the general and specific factors themselves, Bayes's rule gives the posterior distribution for the factors, which will put more weight on some of these possibilities than others, but that ranking comes solely from the prior. If we decide a priori that case (i) is more probable than case (ii), then our posterior estimates will reflect this. It's hard to see what non-circular grounds we'd have for such a decision. (Empirical Bayes doesn't seem to help.)
Of course, if one makes up the general factor so that it's a linear combination of the observed test scores, as in modern exploratory factor analysis, then the general factor is, by definition, calculable from the data. Unfortunately, using a different battery of tests would give you a different common factor, and these will not, except by sheer luck, agree.
Peter Schonemann has written extensively on this problem, and may be the best starting point if you want to know more. (His paper "Factorial Definitions of Intelligence" [abstract, PDF] reproduces Wilson's review as an appendix.) I give this consideration less weight than he does. (So, apparently, does his sometime-collaborator J. H. Steiger.) It definitely rules out claims that g gives us an operational and measurable definition of general intelligence. It does not rule out factor analysis as a means of discovering causal structure. If factor analysis could do that, the fact that it couldn't also give us precise estimates (even in the limit) of the causal variables it found would be unfortunate, but we would still know they mattered, and that should encourage us to find ways of measuring them directly.
[3]: Spearman advocated making the right to vote contingent on demonstrating at least a certain minimum level of general intelligence, on the grounds that stupid people cannot exercise political judgment. Implicit in this is the idea that democracy is justified only to the extent that it makes the right decision or picks the best rulers, which I find repugnant; the point of democracy ought to be that it gives people power over their own lives, and makes rulers accountable to the ruled. (That it also tends to lead to better decisions and more social power helps it survive, but those aren't the point.) On his own theoretical principles, however, all Spearman should have cared about was the sum of the general factor and a specific factor of political judgment, not either factor alone.
[4] I recommend Loehlin's Latent Variable Models: An Introduction to Factor, Path, and Structural Analysis to students who need to know more, since it's clear, practical, decent on the strengths and limitations of the methods, sound on the need for statistical power, and written in an actual human voice. My copy is the second edition; I'm told, but haven't checked, that the fourth finally updated the vintage MacDraw diagrams. Loehlin has been contributing to the literature on IQ and its heritability since the 1970s, at least, and is far more of a hereditarian than I am, though not of the creepy (i.e., Jensenist) school — see e.g. Loehlin, Lindzey and Spuhler, Race Differences in Intelligence (W. H. Freeman, 1975), which contains some useful criticisms of, e.g., Leon Kamin.
— This paper by Bartholomew is a nice over-view from a statistician's perspective, but the implication (in the abstract) that graphical models neglect latent variables is more than a little boggling, and his description of Thomson's model (of which much more below) is not altogether accurate.
[5]: Somewhat more seriously, you can choose whether to make the constructed factors have correlations amongst themselves or be uncorrelated, to prefer factors which involve only a few observations or factors which involve many, etc. There are elaborate techniques ("rotations") for turning factor models which do well by one of these standards into ones which are better by another criterion, all the while giving you completely equivalent observational results, at least at the level of means and correlations. Stephen Jay Gould, in The Mismeasure of Man, made a big deal out of this point. This has met with a lot of objection, sometimes by people saying that one particular way of rotating the factors is correct, and sometimes by people saying that correlations among the factors would need to be explained by other factors in turn ("hierarchical factor analysis"), and doing so just amounts to admitting that there is a general factor g after all. Who was right about this is, however, quite irrelevant here.
As a footnote to this footnote, however, let me point out that even if (miraculously) hierarchical factor analysis gets at the causal structure, it can give you very different kinds of causes at different levels. Suppose for example, that there really were just three distinct skills tapped by intelligence tests — verbal ability, spatial ability, and problem-solving ability. Suppose further (for clarity, not plausibility) that these three abilities were localized in completely distinct parts of the brain, that genes which influenced one had no effect on the others, that they could be trained separately without any transfer of learning, etc. One would then say that these were, indeed, causally distinct and separable talents. They might nonetheless well be positively correlated in a factor analysis, because certain environmental influences would affect them all the same way (nutrition, disease, stress), and even if there was no transfer of training, social processes would tend to correlate verbal schooling with, say, schooling in problem-solving. The higher-level factor associated with their correlations would then just be something like "quality of the developmental environment", and not another, more general mental ability.
[6]: Technically, what I'm showing here is a principle component analysis, rather than a factor analysis in the strict sense. PCA finds linear combinations of the original variables which (1) are uncorrelated and (2) describe as much of the variance as possible, maximizing our ability to reconstruct the original variables. Factor analysis, in the Spearman-Thurstone-etc. sense, aims to describe the correlations of the variables, not their actual values. If I do a strict factor analysis of this data with two factors, the first looks more or less the same as the first principle component (which is not surprising), but the second factor does not, and it's very hard to come up with any meaningful interpretation of it. (This is so no matter what rotation algorithm I try.)
[7]: Which I only learned about from a chance encounter with his 1939 book on The Factorial Analysis of Human Ability at a library booksale; I'm not an expert on the history here. (One doesn't have to be to see the logical problems.) It is striking how many of even the more technical difficulties which Thomson raised there remain issues with factor analysis: underdetermination of factor values, the inability of correlations to distinguish between different analyses, the dependence of estimated factors and factor loadings on accidents of test construction and the population tested, the neglect of statistical power when evaluating analyses, etc.
Thomson's description in Factorial Analysis of his sampling model is mostly concerned with the case where the variables are binary, which simplifies some calculations but obscures the general point. In part this was because he was identifying his variables with the "bonds" of Thorndike's proto-connectionism; he does not explain this to readers, evidently supposing them to be familiar with it. (See note 14 below for more.)
Thomson's original paper ("A Hierarchy without a General Factor", British Journal of Psychology 8 (1916): 271--281), reporting results he obtained in 1914, does not seem to be available electronically, but a follow-up ("On the Cause of Hierarchical Order among the Correlation Coefficients of a Number of Variates Taken in Pairs", Proceedings of the Royal Society of London A 95 (1919): 400--408) is in JSTOR, and worth reading.
[8] The reason is more technical than the rest, so I'll stick it in this footnote. The correlations among the components in an intelligence test, and between tests themselves, are all positive, because that's how we design tests. But that means that the correlation matrix only has positive entries. This has implications for factor analysis, because the usual way of finding the factors is to take the eigenvectors of the correlation matrix (after an adjustment which reduces the diagonal entries but leaves them positive). The larger the corresponding eigenvalue, the more of the variance is described by that eigenvector. The Frobenius-Perron Theorem, however, tells us that any matrix with all-positive entries has a unique largest eigenvalue, and that the corresponding eigenvector only has positive entries. (If some of the correlations are allowed to be zero, there can be multiple eigenvectors which all have the largest eigenvalue, and all their components are non-negative.) Translated into factor analysis: there has to be a factor which describes more of the variance than any other, and every variable is positively loaded on it. So making up tests so that they're positively correlated and discovering they have a dominant factor is just like putting together a list of big square numbers and discovering that none of them is prime — it's necessary side-effect of the construction, nothing more. However, the Frobenius-Perron Theorem doesn't say by how much the largest factor has to dominate. What my little simulations show is that in completely random cases it can dominate quite a lot, and this can happen even when the theorem doesn't apply (because some correlations are negative).
Similarly for hierarchical factor analysis. Wim Krijnen ("Positive Loadings and Factor Correlations from Positive Covariances", Psychometrika 69 (2004): 655--660) has algebraically proved what was intuitively clear, that an all-positive correlation matrix is itself sufficient to ensure that there will be a single higher-order factor, with positive loadings on the lower-order factors. Given this fact, the occasional dispute about whether g is a second-order or third-order factor seem not so much like debating how many angels can dance on the head of a pin, as like assuming that there must be an angel, since the pin after all comes to a single sharp point, and debating the angel's place in the celestial hierarchy.
[9] The entries above the diagonal were picked uniformly and independently on the interval from 0 to 1; those below the diagonal are their mirror images (because correlations are symmetric); and the diagonal itself is 1 (because everything is perfectly correlated with itself). I had R generate matrices according to that procedure until it came up with one which was also positive definite, as a correlation matrix must be; this was just the first output of the random number generator which wasn't rejected. You can see how I implemented the test in my code. That code also includes an option for generating correlation matrices which are not just symmetric and positive-definite but also diagonally dominated.
The "test scores" of the subjects were Gaussian random vectors, with the prescribe correlations, a mean on each dimension of 100 and a standard deviation on each dimension of 15. Each vector was independent of all the other vectors.
[10]: It's worth doing a quick check that I haven't, by chance, produced a set of correlations which "really" are all due to a single factor, whatever that would mean here. If that was the case, the correlation between any two variables should be the product of their factor loadings. Some are close, e.g., variables 1 and 3 have a correlation of 0.683, and that would predict (0.782)*(0.814) = 0.637, but others are way too far off, e.g., 1 and 5, where (0.782)*(0.669) = 0.523, more than twice the real value of 0.241. The chi-squared statistic for testing the hypothesis that there is only one factor, and all apparent partial correlations are due to chance, is 1023.81 on 5 degrees of freedom, which translates to a p-value of about 4 * 10-219.
[11] I am also assuming that you don't do something silly like sample the tail of one of the variables. In my random data, if I confine myself to the samples where the first variable is > 120, I find that the correlation between variable 1 and variable 5 is not 0.241, but 0.017, and the correlation between variables 2 and 5 is not 0.002 but -0.161. This is, or ought to be, a duh. (If you want to see the point really driven home, or to see just how much it can screw up your factor analyses, consult the chapters on sampling of test-takers in Thomson's Factorial Analysis.)
[12]: Here is another example of the same effect. We now have complete DNA sequences for a number of people, including James Watson. So in principle we could do the experiment were we take a large group of people, and take samples of some 10 or 100 or 1000 different cell types from each, and identify which of, say, 5000 different genes are being expressed in each cell type in each person. The cell type gets one point for each expressed gene which is different from the version in Watson's genome. The score of each cell type will thus depend on many factors, some shared (genes expressed across many or all cell types) and some specific. Now extract the leading factor. Mathematically, it will exist, and it will even be heritable. It's also quite meaningless biologically, even as an index of not-James-Watson-ness. [This paragraph was written in the summer of 2007, well before the latest brouhaha over Watson's views on the stupidity of black people.]
[13]: To see the follies such circularity leads to, compare this post by Tyler Cowen with the scoldings he gets in his comments section. Cowen points out behaviors which call for intelligence, in the ordinary meaning of the word, and that these intelligent people would score badly on IQ tests. A reasonable counter-argument would be something like: "It's true that 'intelligence', in the ordinary sense, is a very broad and imprecise concept, and it's not surprising the tests don't capture it perfectly. But the aspects of 'intelligence' they do capture are ones which are vastly more important for economic development than the ones displayed by Cowen's friends in San Agustin Oapan, however amiable or even admirable those traits might be in their own right." This would be a position about which one could have a rational argument. (Indeed, I might even agree with that statement, as far as it goes, as might A. R. Luria.) Instead, Cowen gets told over and over that if it's not showing up in IQ it's not intelligence, and it's unscientific and sentimental of him to think otherwise.
And people wonder why I don't set up comments.
[14]: It's not really relevant to the question at hand, but I should say a little about the neural interpretation Thomson gave his model. He tended to think of what I've been calling the abilities as "on the bodily side ... neurone arcs" (Factorial Analysis, p. 271), and to think, by analogy with the all-or-none firing of individual neurons, that they should be binary variables (p. 54). Highly g-loaded questions and tests were thus ones which engaged large parts of the brain, or at least (pp. 50ff) large fractions of the part of the brain which could be probed with intelligence tests. Following the general trend of neuroscientific opinion in his day, he thought the brain had little, if any, important localization of function, though he allowed that there could be several "sub-pools". (There were actually good reasons, based on experiments, for people to take this view, which was nonetheless wrong. Anne Harrington's books — Medicine, Mind, and the Double Brain and Reenchanted Science — provide nice historical perspectives.) But, of course, all this is an interpretation of the stochastic model, not the model itself; if I really wanted to push for a revival of the model — which I don't — I'd prefer to interpret the abilities as how well different specialized cognitive modules function, along with some invocation of the distributed nature of neural information processing.
[15]: There are a very narrow set of technical conditions which let you out of this, i.e., which let you combine group differences, measurement unbiasedness and predictive unbiasedness. (See Millsap's papers for details.) That IQ tests satisfy them is highly implausible, and, to say the least, empirically unsupported. If someone wants to show that IQ tests are unbiased, that's what they need to be working on, not pounding their tables of regression coefficients.
[16] This is not to endorse Fagan's theory of intelligence, which seems to me far too simple as well. Also, that paper sticks to the same sort of linear regression/ANOVA/etc. techniques as the others in such journals, which, as I keep saying, have a lot of problems. But, again, if you find Arthur Jensen's methods acceptable, let alone Richard Lynn's or Philippe Rushton's or Charles Murray's, then you really have no right to quibble, and (unlike those three) Fagan and Holland at least do basic covariate matching.
Manual trackback: Crooked Timber; Uncertain Principles; Pharyngula; Chrononautic Log; Pure Pedantry; Exploding Galaxies; Nanopolitan; Pyjamas in Bananas; Danny Yee; Existence Is Wonderful; Crooked Timber (again); Lawyers, Guns and Money; 3 Quarks Daily; Siris; Quantum of Wantum; Entitled to an Opinion; ArchPundit; Raw Thought; Idiolect; Boîte noire; Dissecting Leftism; The Ministry of Science; LanguageLog; Noli Irritare Leones; Work for Idle Hands; Green Apron Monkey; It Makes an Ancient Rumbling Sound; EphBlog; Medical Humanities Blog; Ars Mathematica; Crooked Timber (once more, with feeling this time); Jewcy; Lean Left; The Jed Report; Ezra Klein; The Mahatma X Files; Quantum of Wantum; Language Log (again); Social Science Statistics Blog; The Inverse Square Blog; The Useless Tree; Revelations of Silence; Robert Lindsay; Sequential Effects; Adrift in the Happy Hills; The Learner; Strongly Emergent; Quomodocumque; Slate Star Codex (context); The Last Conformer; [citation needed]Minor updates 19 October: Fixed typos, broken link to Millsap and Meredith's paper (thanks to Bill Raynor). 22 October: Fixed typos (thanks to Dave Kane). 19 November: Fixed typos (thanks to Jutta Degener).
Enigmas of Chance; The Natural Science of the Human Species; Minds, Brains, and Neurons; IQ
Posted at October 18, 2007 17:20 | permanent link