Three-Toed Sloth

This Climate Goes to Eleven

Gerard H. Roe and Marcia B. Baker, "Why Is Climate Sensitivity So Unpredictable?", Science 318 (2007): 629--632 [no free copy]

Abstract: Uncertainties in projections of future climate change have not lessened substantially in past decades. Both models and observations yield broad probability distributions for long-term increases in global mean temperature expected from the doubling of atmospheric carbon dioxide, with small but finite probabilities of very large increases. We show that the shape of these probability distributions is an inevitable and general consequence of the nature of the climate system, and we derive a simple analytic form for the shape that fits recent published distributions very well. We show that the breadth of the distribution and, in particular, the probability of large temperature increases are relatively insensitive to decreases in uncertainties associated with the underlying climate processes.

Roe and Baker's argument is simple but ingenious and compelling. The climate system contains a lot of feedback loops. This means that the ultimate response to any perturbation or forcing (say, pumping 20 million years of accumulated fossil fuels into the air) depends not just on the initial reaction, but also how much of that gets fed back into the system, which leads to more change, and so on. Suppose, just for the sake of things being tractable, that the feedback is linear, and the fraction fed back is f. Then the total impact of a perturbation J is

J + Jf + Jf² + Jf³ + ... The infinite series of tail-biting feedback terms is in fact a geometric series, and so can be summed up if f is less than 1: J/(1-f) (If f is greater than 1, then the feedback goes off to infinity; I'll come back to that.)

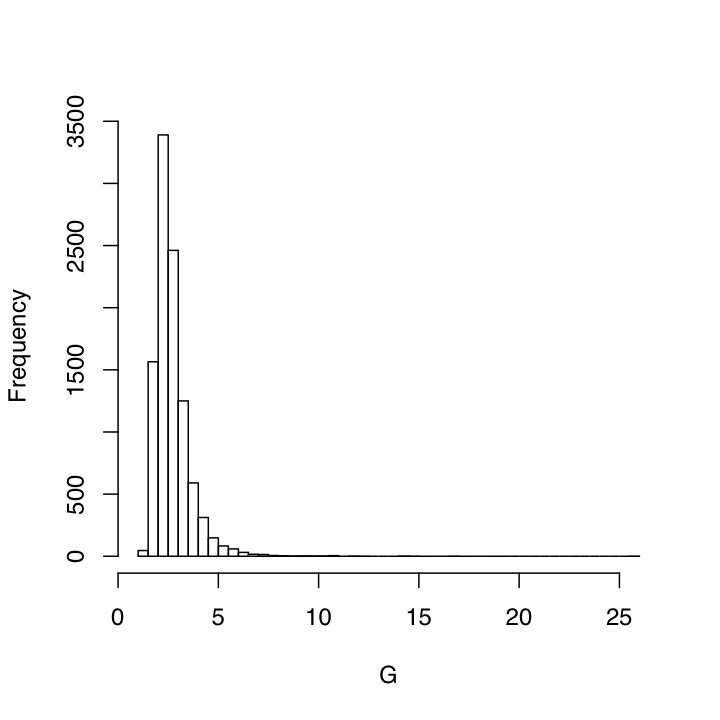
If we knew the value of the feedback f, we could predict the response to perturbations just by multiplying them by 1/(1-f) — call this G for "gain". What happens, Roe and Baker ask, if we do not know the feedback exactly? Suppose, for example, that our measurements are corrupted by noise --- or even, with something like the climate, that f is itself stochastically fluctuating. The distribution of values for f might be symmetric and reasonably well-peaked around a typical value, but what about the distribution for G? Well, it's nothing of the kind. Increasing f just a little increases G by a lot, so starting with a symmetric, not-too-spread distribution of f gives us a skewed distribution for G with a heavy right tail.

To illustrate, here is a histogram made from drawing 10,000 random numbers from a Gaussian distribution with mean 0.6 and a standard deviation of 0.1; think of these as the values of f, the strength of the feedback.

It's pretty symmetric: the values in the bottom quarter run from about 0.25 to 0.53, a spread of 0.28, and those in the top quarter run from 0.67 to 0.96, a spread of 0.29.

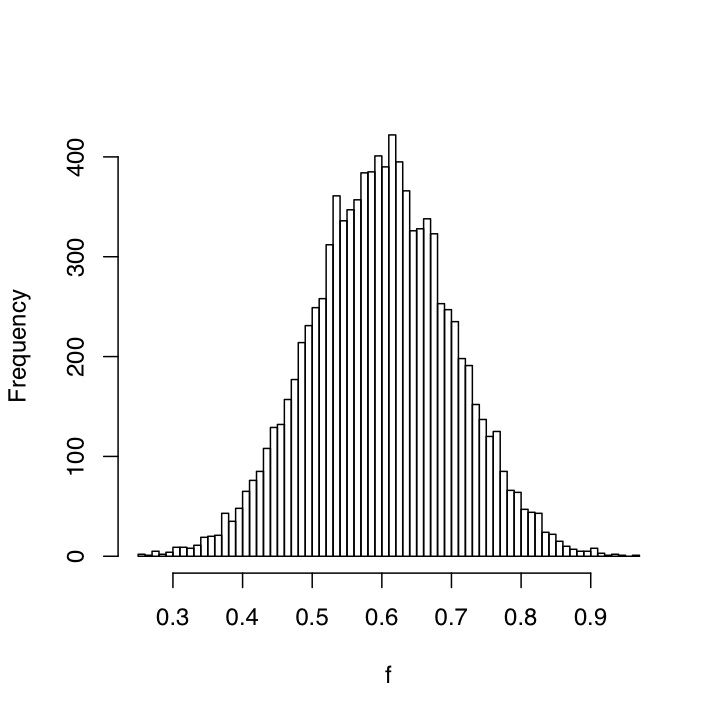
And here is the histogram of the corresponding values of G, the over-all gain.

It's not symmetric at all: the bottom quarter of values run from 1.3 to 2.1, a range of 0.8, but the top quarter runs from 3.0 to almost 26. The probability that the gain is substantially above the median or even mean value is quite substantial, because of this skew to the right.

If we can reduce the uncertainty in f, then of course the distribution of G will also narrow, but much more slowly than you might think. Here is what things look like when the standard deviation of f is cut by a half, to 0.05:

and the corresponding plot for G: The top quartile now starts at 2.7, rather than 3.0, and runs only up to 5, rather than 26, but that just means that things might just be twice as bad as the base-line projection, rather than ten times as bad. We would have to know f incredibly accurately for the uncertainty in G to be a matter of "plus or minus", rather than "to within a factor of".

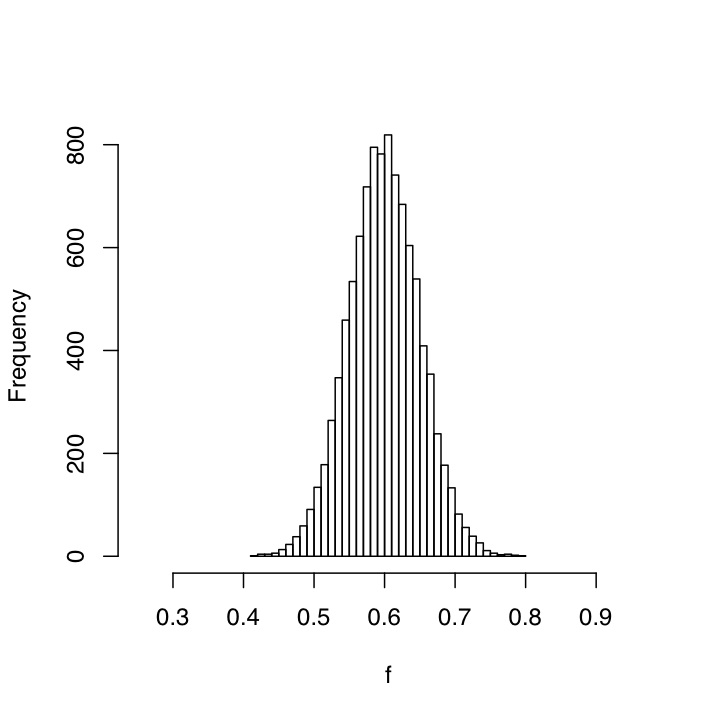
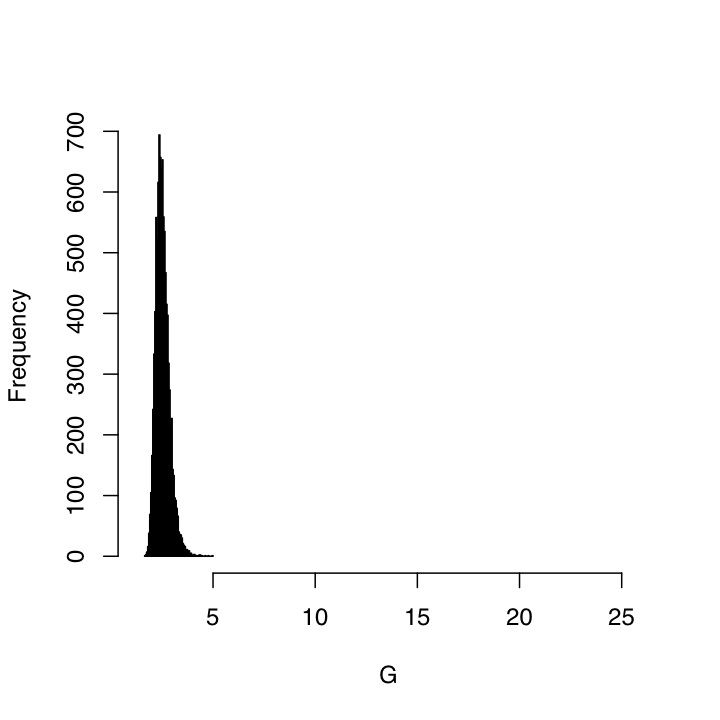
A few points seem worth making here.

1. This is all assuming straightforward linear feedbacks, which are on the whole positive. This means it applies to any feedback system. Very trivially, it'll make a nice homework problem.
2. Linear feedback is at best an approximation. It would be interesting to see what happens if one includes nonlinear feedback, including the possibility for temporarily runaway positive feedback. (Snowball earth and all that.)
3. Roe and Baker claim that the uncertainty in f is dominated by the uncertainty in the least-certain feedback process, even if it doesn't make a dominant contribution to the total feedback. This sounds like it assumes linearity; I'd like to know whether it's still true in a strongly nonlinear situation.
4. Even if we're in an approximately linear feedback regime, there is a lot of plausibility to the idea that the feedback factor is actually stochastically fluctuating --- or least, that it fluctuates in response to forces which change too fast to be systematically predicted from other parts of a climate model, which comes to much the same thing.
5. I can't see how adding fancy nonlinear dynamics could make things any more predictable.
6. Finally, the whole analysis can be repeated using confidence intervals rather than random variables. It'd be very interesting to think about how to construct properly-calibrated frequentist prediction intervals here.
7. I am not sure whether this qualifies as an instance of the pattern "positive feedback leading to highly skewed distributions". Maybe there's a common mathematical core to this and e.g. Simon's work on skew distributions, but if so it's not leaping out at me.

In short: the fact that we will probably never be able to precisely predict the response of the climate system to large forcings is so far from being a reason for complacency it's not even funny.

Update, 27 November: I should have linked to the discussion of this paper over on RealClimate initially.

Manual trackback: Earning My Turns; Political Animal; Coyote Blog; A Change in the Wind; That's Almost Right

Enigmas of Chance