Notebooks

Chains with Complete Connections

Last update: 08 Dec 2024 00:28
First version: 1 August 2016

\[ \newcommand{\indep}{\mathrel{\perp\llap{\perp}}} \]

"Chain with complete connections" is an ungainly name for an important class of stochastic process, closely related to Markov and hidden-Markov models (HMMs).

In an ordinary (discrete-time) Markov process, we have a sequence of random variables \( S_0, S_1, \ldots S_t, \ldots \), where the future is conditionally independent of the past, given the present: \[ S_{t+1}^{\infty} \indep S^{t-1}_{-\infty} | S_t \] Now let's add an additional sequence of random variables, say \( X_t \), where each \( X_{t+1} \) is a random function of \( S_t \) alone, i.e., \[ X_{t+1} \indep \{ X^{t}_{-\infty}, S^{t-1}_{-\infty} \} | S_t \] So far, this is the usual set up for HMMs. What makes chains with complete connections special is that there is a deterministic function, say \( q \), where \[ S_{t+1} = q(S_t, X_{t+1}) \] That is, the next state is determined by the current state and the observation which that state produces. Notice that this means the sequence of pairs \((S_t, X_t) \) is also a Markov process. The \( X_t \) process, however, is not necessarily Markovian, and in fact generally isn't.

The difference between CCCs and HMMs can is perhaps clearer with a graphical model:

HMM
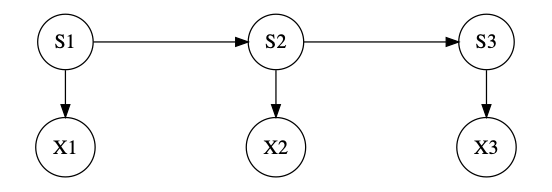
CCC

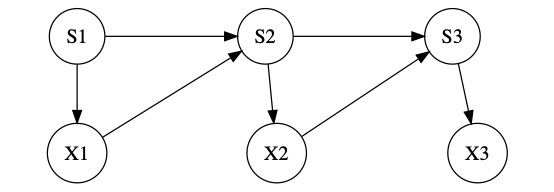
On the other hand, here's an example to show that a CCC isn't necessarily a Markov chain at any order. Take two states, call them 1 and 2. State 1 flips a coin and produces either A or B. If it produces A, it goes back to A; if it produces B, it goes to state 2. State 2 always produces a B, and goes back to state 1. (That is, \( S_t \) can be either 1 or 2, and \( X_t \) can be either A or B.) This, too, can be illustrated by a picture, but it's a state-transition diagram, not a variable-dependence graphical model:

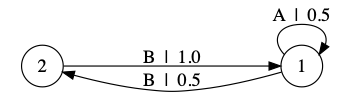
(The first two diagrams used the visual conventions for graphical models, where nodes are variables and arrows indicate direct dependence; this one uses the visual conventions for automata theory / Markov models, where nodes are states and arrows are transitions, labeled with the observations made on each transition. I realize it's bad pedagogy to switch visual conventions from one figure to the next...)

This process will produce blocks of Bs of even length, separated by blocks of As of arbitrary length. But then the conditional distribution of the next observation changes depending on whether it was proceeded by an even or an odd number of Bs, which can't be determined from any fixed, finite history, hence the observable process isn't Markov at any finite order. (The length of history we need for context is however almost-surely finite.) This example is, I was told, originally invented by Benjamin Weiss in the 1970s, and called the "even process", though I haven't verified those references.

I find this class of processes interesting for a couple of reasons. One is that it is very natural for lots of processes, like urn processes, or many models of learning in animals. (Think of the state as being the probability of making different actions, which in turn lead to different rewards, and so to changing the probabilities of those actions.) The other is that just about any stochastic process can be represented in this form, where the hidden states are actually the optimal predictions for the original process. But that subject is involved enough to deserve its own notebook.

--- "Sofic processes" are a special case. (Or, rather, what the symbolic dynamics literature calls right-resolving presentations of sofic processes are.)

--- Cox's 1981 distinction between "parameter-driven" and "observation-driven" models of time series corresponds, in intent at least, to that between ordinary HMMs and chains with complete connections, respectively.

permanent link for this note   RSS feed for this note

Notebooks: