Three-Toed Sloth

The Distribution of Library Book Circulation Is Not a Power Law, or, Gauss and Man at Huddersfield

Via Bill Tozier comes news of this blog post by Eric Hellman, which is part of a controversy over how libraries should pay publishers for electronic books. I have not thought or studied that enough to have any sort of opinion, though since it seems to go very, very far from marginal cost pricing, I am naturally suspicious. Be that as it may, Hellman suggests that the specific proposal of Harper Collins needs to be seen in the light of the "long tail" of the circulation distribution of library books. That is, most books circulate very little, while a few circulate and awful lot, accounting for a truly disproportionate share of the circulation, and (says Hellman) the Harper Collins proposal would, compared to the status quo, shift library funds from the publishers of the large mass of low-circulation books to the publishers of the tail of high-circulation books, Harper Collins prominent among them.

To support this, Hellman uses some data from a very rich data set released by the libraries of the University of Huddersfield in England. (I have been meaning to look this up since Magistra et Mater mentioned the cool stuff Huddersfield is doing with library data-mining.) Hellman's analysis went as follows. (See his post for details.) He made a cumulative histogram of how often each book had circulated (binning counts over 100 by tens); plotted it on a log-log scale; fit a straight line by least squares; and declared the distribution a power law because the R² was so high.

Constant readers can imagine my reaction.

Having gotten hold of the data, I plotted the cumulative distribution function (without binning), and including both Hellman's power law (purple), and a discrete log-normal distribution (red):

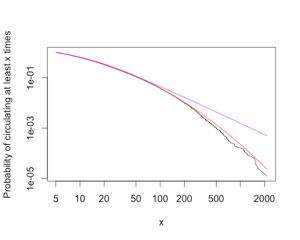
This is clearly heavy tailed and massively skewed to the right. It is equally clear that it is not a power law: there are simply orders of magnitude too few books which circulated 500 or 1000 or 2000 times. (Remember that the vertical axis here is on a log scale.) The difference in log-likelihoods is 200 in favor of log-normal, i.e, the data were e²⁰⁰ times less likely under the power law. Applying the non-nested model comparison test from my paper with Aaron and Mark, the chance this big a difference in likelihoods arising through fluctuations when the power law is actually as good or better than the log-normal is about 10^-35. I have not attempted to see whether the deviations from the log-normal curve are significant, but it does look quite good over almost the whole range of the data. There could be some systematic departures at the far right, but over-all it looks like Gauss is not mocked at Huddersfield.

I should say right away that Hellman was very gracious in our correspondence about this (I am after all a quibbling pedant quite unknown to him). More importantly, his analysis of the Harper Collins proposal does not, that I can see, depend at all on circulation following a power law; it just has to be strongly skewed to the right. That being the case, I hope this particular power law can be eradicated before it has a chance to become endemic in such permanent reservoirs of memetic infection as the business literature and Physica A.

Update, next day: In the interests of reproducibility, the circulation totals for the data (gzipped), and the R code for my figure. The latter needs the code from our paper, which I will turn into a proper R package Any Time Now.

Previously on "Those That Resemble Power Laws from a Distance": the link distribution of weblogs (and again); the distribution of time taken to reply to e-mail; the link distribution of biochemical networks; urban economies in the US.

Power Laws