Three-Toed Sloth

Any P-Value Distinguishable from Zero is Insufficiently Informative

\[ \newcommand{\Prob}[1]{\mathbb{P}\left( #1 \right)} \newcommand{\Probwrt}[2]{\mathbb{P}_{#1}\left( #2 \right)} \newcommand{\Var}[1]{\mathrm{Var}\left[ #1 \right]} \]

Attention conservation notice: 4900+ words, plus two (ugly) pictures and many equations, on a common mis-understanding in statistics. Veers wildly between baby stats. and advanced probability theory, without explaining either. Its efficacy at remedying the confusion it attacks has not been evaluated by a randomized controlled trial.

After ten years of teaching statistics, I feel pretty confident in saying that one of the hardest points to get through to undergrads is what "statistically significant" actually means. (The word doesn't help; "statistically detectable" or "statistically discernible" might've been better.) They have a persistent tendency to think that parameters which are significantly different from 0 matter, that ones which are insignificantly different from 0 don't matter, and that the smaller the p-value, the more important the parameter. Similarly, if one parameter is "significantly" larger than another, then they'll say the difference between them matters, but if not, not. If this was just about undergrads, I'd grumble over a beer with my colleagues and otherwise suck it up, but reading and refereeing for non-statistics journals shows me that many scientists in many fields are subject to exactly the same confusions as The Kids, and talking with friends in industry makes it plain that the same thing happens outside academia, even to "data scientists". (For example: an A/B test is just testing the difference in average response between condition A and condition B; this is a difference in parameters, usually a difference in means, and so it's subject to all the issues of hypothesis testing.) To be fair, one meets some statisticians who succumb to these confusions.

One reason for this, I think, is that we fail to teach well how, with enough data, any non-zero parameter or difference becomes statistically significant at arbitrarily small levels. The proverbial expression of this, due I believe to Andy Gelman, is that "the p-value is a measure of sample size". More exactly, a p-value generally runs together the size of the parameter, how well we can estimate the parameter, and the sample size. The p-value reflects how much information the data has about the parameter, and we can think of "information" as the product of sample size and precision (in the sense of inverse variance) of estimation, say \( n/\sigma^2 \). In some cases, this heuristic is actually exactly right, and what I just called "information" really is the Fisher information.

Rather than working on grant proposals Egged on by a friend As a public service, I've written up some notes on this. Throughout, I'm assuming that we're testing the hypothesis that a parameter, or vector of parameters, \( \theta \), is exactly zero, since that's overwhelming what people calculate p-values for --- sometimes, I think, by a spinal reflex not involving the frontal lobes. Testing \( \theta=\theta_0 \) for any other fixed \( \theta_0 \) would work much the same way. Also, \( \langle x, y \rangle \) will mean the inner product between the two vectors.

1. Any Non-Zero Mean Will Become Arbitrarily Significant

Let's start with a very simple example. Suppose we're testing whether some mean parameter \( \mu \) is equal to zero or not. Being straightforward folk, who follow the lessons we were taught in our one room log-cabin schoolhouse research methods class, we'll use the sample mean \( \hat{\mu} \) as our estimator, and take as our test statistic \( \frac{\hat{\mu}}{\hat{\sigma}/\sqrt{n}} \); that denominator is the standard error of the mean. If we're really into old-fashioned recipes, we'll calculate our p-value by comparing this to a table of the \( t \) distribution with \( n-2 \) degrees of freedom, remembering that it's \( n-2 \) because we're using one degree of freedom to get the mean estimate (\( \hat{\mu} \)) and another to get the standard deviation estimate (\( \hat{\sigma} \)). (If we're a bit more open to new-fangled notions, we bootstrap.) Now what happens as \( n \) grows?

Well, we remember the central limit theorem: \( \sqrt{n}(\hat{\mu} - \mu) \rightarrow \mathcal{N}(0,\sigma^2) \). With a little manipulation, and some abuse of notation, this becomes \[ \hat{\mu} \rightarrow \mu + \frac{\sigma}{\sqrt{n}}\mathcal{N}(0,1) \] The important point is that \( \hat{\mu} = \mu + O(n^{-1/2}) \). Similarly, albeit with more algebra, \( \hat{\sigma} = \sigma + O(n^{-1/2}) \). Now plug these in to our formula for the test statistic: \[ \begin{eqnarray*} \frac{\hat{\mu}}{\hat{\sigma}/\sqrt{n}} & = & \sqrt{n}\frac{\hat{\mu}}{\hat{\sigma}}\\ & = & \sqrt{n}\frac{\mu + O(n^{-1/2})}{\sigma + O(n^{-1/2})}\\ & = & \sqrt{n}\left(\frac{\mu}{\sigma} + O(n^{-1/2})\right)\\ & = & \sqrt{n}\frac{\mu}{\sigma} + O(1) \end{eqnarray*} \] So, as \( n \) grows, the test statistic will go to either \( +\infty \) or \( -\infty \), at a rate of \( \sqrt{n} \), unless \( \mu=0 \) exactly. If \( \mu \neq 0 \), then the test statistic eventually becomes arbitrarily large, while the distribution we use to calculate p-values stabilizes at a standard Gaussian distribution (since that's a \( t \) distribution with infinitely many degrees of freedom). Hence the p-value will go to zero as \( n\rightarrow \infty \), for any \( \mu\neq 0 \). The rate at which it does so depends on the true \( \mu \), the true \( \sigma \), and the number of samples. The p-value reflects how big the mean is (\( \mu \) \), how precisely we can estimate it (\( \sigma \)), and our sample size (\( n \)).

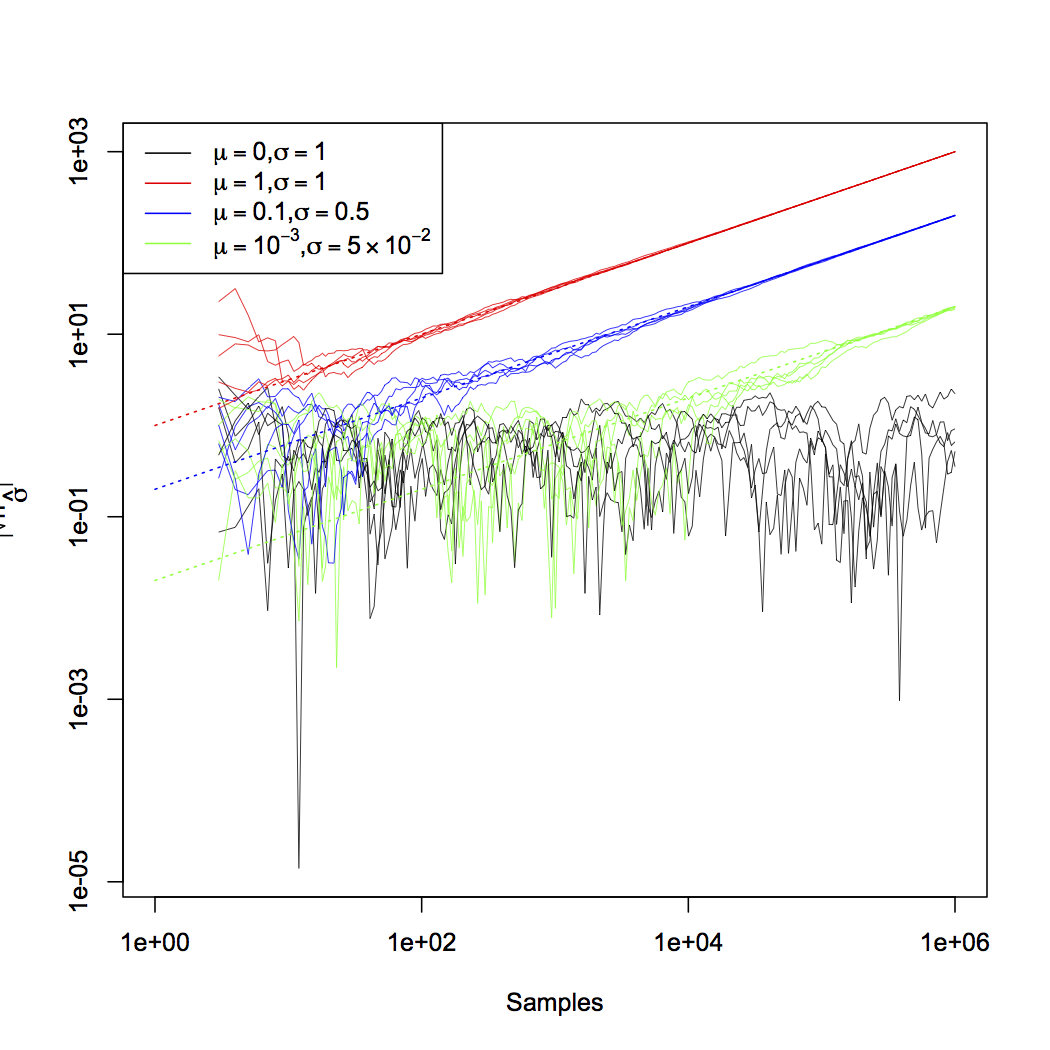
T-statistics calculated for five independent runs of Gaussian random variables with the specified parameters, plotted against sample size. Successive t-statistics along the same run are linked; the dashed lines are the asymptotic formulas, \( \sqrt{n}\mu/\sigma \). Note that both axes are on a logarithmic scale. (Click on the image for a larger PDF version; source code.)

2. Any Non-Zero Regression Coefficient Will Become Arbitrarily Significant

Matters are much the same if instead of estimating a mean we're estimating a difference in means, or regression coefficients, or linear combinations of regression coefficients ("contrasts"). The p-value we get runs together the size of the parameter, the precision with which we can estimate the parameter, and the sample size. Unless the parameter is exactly zero, as \( n\rightarrow\infty \), the p-value will converge stochastically to zero.

Even if two parameters are estimated from the same number of samples, the one with a smaller p-value is not necessarily larger; it may just have been estimated more precisely. Let's suppose we're in the land of good, old-fashioned linear regression, where \( Y = \langle X, \beta \rangle + \epsilon \), where all the random variables have mean 0 (to simplify book-keeping), where \( \epsilon \) is uncorrelated with \( X \). Estimating \( \beta \) with ordinary least squares, we get of course \[ \hat{\beta} = (\mathbf{x}^T \mathbf{x})^{-1} \mathbf{x}^T \mathbf{y} ~, \] with \( \mathbf{x} \) being the \( n\times 2 \) matrix of \( X \) values and \( \mathbf{y} \) the \( n\times 1 \) matrix of \( Y \) values. Since \( \mathbf{y} = \mathbf{x} \beta + \mathbf{\epsilon} \), \[ \hat{\beta} = \beta + (\mathbf{x}^T \mathbf{x})^{-1}\mathbf{x}^T \mathbf{\epsilon} ~. \] Assuming the \( \epsilon \) terms are uncorrelated with each other and have constant variance \( \sigma^2_{\epsilon} \), we get \[ \Var{\hat{\beta}} = \sigma^2_{\epsilon} (\mathbf{x}^T \mathbf{x})^{-1} ~. \] To understand what's really going on here, notice that \( \frac{1}{n} \mathbf{x}^T \mathbf{x} \) is the sample variance-covariance matrix of \( X \); call it \( \hat{\mathbf{v}} \). (I give it a hat because it's an estimate of the population covariance matrix.) So \[ \Var{\hat{\beta}} = \frac{\sigma^2_{\epsilon}}{n}\hat{\mathbf{v}}^{-1} \] The standard errors for the different components of \( \hat{\beta} \) are thus going to be the square roots of the diagonal entries of \( \Var{\hat{\beta}} \). We will therefore estimate different regression coefficients to different precisions. To make a regression coefficient precise, the predictor variable it belongs to should have a lot of variance, and it should have little correlation with other predictor variables. (If we used an orthogonal design, \( \hat{\mathbf{v}}^{-1/2} \) will be a diagonal matrix whose entries are the reciprocals of the regressors' standard deviations.) Even if we think that the size of entries in \( \beta \) is telling us something about how important different \( X \) variables are, one of them having a bigger variance than the other doesn't make it more important in any interesting sense.

3. Consistent Hypothesis Tests Imply Everything Will Become Arbitrarily Significant

So far, I've talked about particular cases --- about estimating means or linear regression coefficients, and even using particular estimators. But the point can be made much more generally, though at some cost in abstraction. Recall that a hypothesis test can make two kinds of error: it can declare that there's some signal when it really looks at noise (a "false alarm" or "type I" error), or it can ignroe the presence of a signal and mistake it for noise (a "miss" or "type II" error). The probability of a false alarm, when looking at noise, is called the size of a test. The probability of noticing a signal when it is present is called the power to detect the signal. A hypothesis test is consistent if its size goes 0 and its power goes to 1 as the number of data points grows. (Purists would call this a consistent sequence of hypothesis tests, but I'm trying to speak like a human being.)

Suppose that a consistent hypothesis test exists. Then at each sample size \( n \), there's a range of p-values \( [0,a_n] \) where we reject the noise hypothesis and claim there's a signal, and another \( (a_n,1] \) where we say there's noise. Since the p-value is uniformly distributed under the noise hypothesis, the size of the test is just \( a_n \), so consistency means \( a_n \) must go to 0. The power of the test is the probability, in the presence of signal, that the p-value is in the rejection region, i.e., \( \Probwrt{\mathrm{signal}}{P \leq a_n} \). Since, by consistency, the power is going to 1, the probability (in the presence of signal) that the p-value is less than any given value eventually goes to 1. Hence the p-value converges stochastically to 0 (again, when there's a signal). Thus, if there is a consistent hypothesis test, and there is any signal to be detected at all, the p-value must shrink towards 0.

I bring this up because, of course, the situations where people usually want to calculate p-values are in fact the ones where there usually are consistent hypothesis tests. These are situations where we have an estimator \( \hat{\theta} \) of the parameter \( \theta \) which is itself "consistent", i.e., \( \hat{\theta} \rightarrow \theta \) in probability as \( n \rightarrow \infty \). This means that with enough data, the estimate \( \hat{\theta} \) will come arbitrarily close to the truth, with as much probability as we might desire. It's not hard to believe that this will mean there's a consistent hypothesis test --- just reject the null when \( \hat{\theta} \) is too far from 0 --- but the next two paragraphs sketch a proof, for the sake of skeptics and quibblers.

Consistency of estimation means that for any level of approximation \( \epsilon > 0 \) and any level of confidence \( \delta > 0 \), for all \( n \geq \) some \( N(\epsilon,\delta,\theta) \), \[ \Probwrt{\theta}{\left|\hat{\theta}_n-\theta\right|>\epsilon} \leq \delta ~. \] This can be inverted: for any \( n \) and any \( \delta \), for any \( \eta \geq \epsilon(n,\delta,\theta) \), \[ \Probwrt{\theta}{\left|\hat{\theta}_n-\theta\right|>\eta} \leq \Probwrt{\theta}{\left|\hat{\theta}_n-\theta\right|>\epsilon(n,\delta,\theta)} \leq \delta ~. \] Moreover, as \( n\rightarrow\infty \) with \( \delta \) and \( \theta \) held constant, \( \epsilon(n,\delta,\theta) \rightarrow 0 \).

Pick any \( \theta^* \neq 0 \), and any \( \alpha \) and \( \beta > 0 \) that you like. For each \( n \), set \( \epsilon = \epsilon(n,\alpha,0) \); abbreviate this sequence as \( \epsilon_n \). I will use \( \hat{\theta}_n \) as my test statistic, retaining the null hypothesis \( \theta=0 \) when \( \left|\hat{\theta}_n\right| \leq \epsilon_n \), and reject it otherwise. By construction, my false alarm rate is at most \( \alpha \). What's my miss rate? Well, again by consistency of the estimator, for any sufficiently small but fixed \( \eta > 0 \), if \( n \geq N(|\theta^*| - \eta, \beta, \theta^*) \), then \[ \Probwrt{\theta^*}{\left|\hat{\theta}_n\right| < \eta} \leq \Probwrt{\theta^*}{\left|\hat{\theta}_n - \theta^*\right|\geq |\theta^*| - \eta} \leq \beta ~. \] (To be very close to 0, \( \hat{\theta} \) has to be far from \( \theta^* \).) So, if I wait until \( n \) is large enough that \( n \geq N(|\theta^*| - \eta, \beta, \theta^*) \) and that \( \epsilon_n \leq \eta \), my power against \( \theta=\theta^* \) is at least \( 1-\beta \) (and my false-positive rate is still at most \( \alpha\)). Since you got to pick pick \( \alpha \) and \( \beta \) arbitrarily, you can make them as close to 0 as we like, and I can still get arbitrarily high power against any alternative while still controlling the false-positive rate. In fact, you can pick a sequence of error rate pairs \( (\alpha_k, \beta_k) \), with both rates going to zero, and for \( n \) sufficiently large, I will, eventually, have a size less thant \( \alpha_k \), and a power against \( \theta=\theta^* \) greater than $\( -\beta_k \). Hence, a consistent estimator implies the existence of a consistent hypothesis test. (Pedantically, we have built a universally consistent test, i.e., consistent whatever the true value of \( \theta \) might be, but not necessarily a uniformly consistent one, where the error rates can be bounded independent of the true \( \theta \). The real difficulty there is that there are parameter values in the alternative hypothesis \( \theta \neq 0 \) which come arbitrarily close to the null hypothesis \( \theta=0 \), and so an arbitrarily large amount of information may be needed to separate them with the desired reliability.)

4. \( p \)-Values for Means Should Shrink Exponentially Fast

So far, I've been arguing that the p-value should always go stochastically to zero as the sample size grows. In many situations, it's possible to be a bit more precise about how quickly it goes to zero. Again, start with the simple case of testing whether a mean is equal to zero. We saw that our test statistic \( \hat{\mu}/(\hat{\sigma}/\sqrt{n}) \rightarrow \sqrt{n}\mu/\sigma + O(1) \), and that the distribution we compare this to approaches \( \mathcal{N}(0,1) \). Since for a standard Gaussian \( Z \) the probability that \( Z > t \) is at most \( \frac{\exp{\left\{-t^2/2\right\}}}{t\sqrt{2\pi}} \), the p-value in a two-sided test goes to zero exponentially fast in \( n \), with the asymptotic exponential rate being \( \frac{1}{2}\mu^2/\sigma^2 \). Let's abbreviate the p-value after \( n \) samples as \( P_n \): \[ \begin{eqnarray*} P_n & = & \Prob{|Z| \geq \left|\frac{\hat{\mu}}{\hat{\sigma}/\sqrt{n}}\right|}\\ & = & 2 \Prob{Z \geq \left|\frac{\hat{\mu}}{\hat{\sigma}/\sqrt{n}}\right|}\\ & \leq & 2\frac{\exp{\left\{-n\hat{\mu}^2/2\hat{\sigma}^2\right\}}}{\sqrt{n}\hat{\mu}\sqrt{2\pi}/\hat{\sigma}}\\ \frac{1}{n}\log{P_n} & \leq & \frac{\log{2}}{n} -\frac{\hat{\mu}^2}{2\hat{\sigma}^2} - \frac{\log{n}}{2n} - \frac{1}{n}\log{\frac{\hat{\mu}}{\hat{\sigma}}} - \frac{\log{2\pi}}{n}\\ \lim_{n\rightarrow\infty}{\frac{1}{n}\log{P_n}} & \leq & -\frac{\mu^2}{2\sigma^2} \end{eqnarray*} \] Since \( \Prob{Z > t} \) is also at least \( \exp{\left\{-t^2/2\right\}}/(t^2+1)\sqrt{2\pi} \), a parallel argument gives a matching lower bound, \( \lim_{n\rightarrow\infty}{n^{-1}\log{P_n}} \geq -\frac{1}{2}\mu^2/\sigma^2 \).

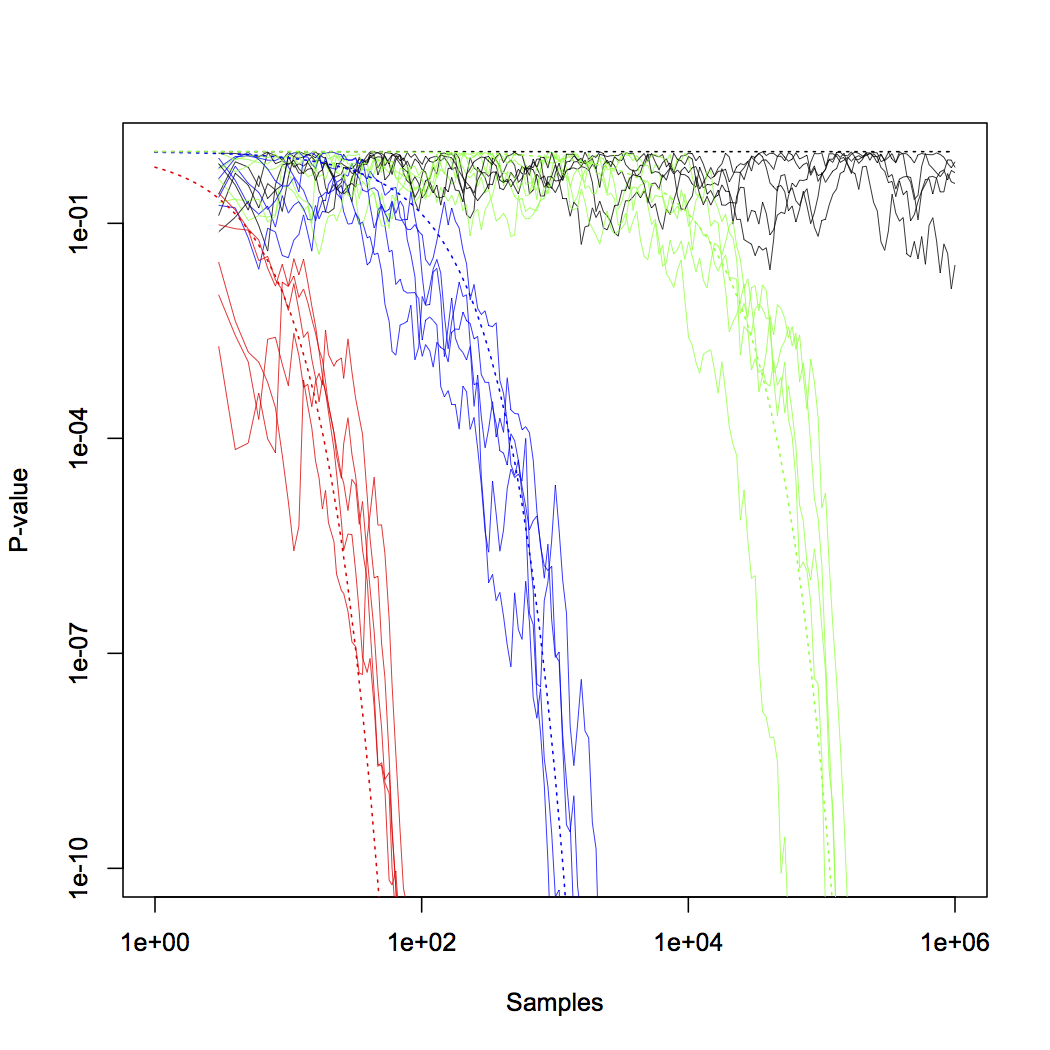
P-value versus sample size, color coded as in the previous figure. Notice that even the runs where \( \mu \), and \( \mu/\sigma \), are very small (in green), the p-value is declining exponentially. Again, click for a larger PDF, source code here.

5. \( p \)-Values in General Will Often Shrink Exponentially Fast

This is not just a cute trick with Gaussian approximations; it generalizes through the magic of large deviations theory. Glossing over some technicalities, a sequence of random variables \( X_1, X_2, \ldots X_n \) obey a large deviations principle when \[ \lim_{n\rightarrow\infty}{\frac{1}{n}\log{\Probwrt{}{X_n \in B}}} = -\inf_{x\in B}{D(x)} \] where \( D(x) \geq 0 \) is the "rate function". If the set \( B \) doesn't include a point where \( D(x)=0 \), the probability of \( B \) goes to zero, exponentially in \( n \),^* with the exact rate depending on the smallest attainable value of the rate function \( D \) over \( B \). ("Improbable events tend to happen in the most probable way possible.") Very roughly speaking, then, \( \Probwrt{}{X_n \in B} \approx \exp{\left\{ - n \inf_{x\in B}{D(x)}\right\}} \). Suppose that \( X_n \) is really some estimator of the parameter \( \theta \), and it obeys a large deviations principle for every \( \theta \). Then the rate function \( D \) is really \( D_{\theta} \). For consistent estimators, \( D_{\theta}(x) \) would have a unique minimum at \( x=\theta \). The usual estimators based on sample means, correlations, sample distributions, maximum likelihood, etc., all obey large deviations principles, at least under most of the conditions where we'd want to apply them.

Suppose we make a test based on this estimator. Under \( \theta=\theta^* \), \( X_n \) will eventually be within any arbitrarily small open ball \( B_{\rho} \) of size \( \rho \) around \( \theta^* \) we care to name; the probability of its lying outside \( B_{\rho} \) will be going to zero exponentially fast, with the rate being \( \inf_{x\in B^c_{\rho}}{D_{\theta^*}(x)} > 0 \). For small \( \rho \) and smooth \( D_{\theta^*} \), Taylor-expanding \( D_\theta^* \) about its minimum suggests that rate will be \( \inf_{\eta: \|\eta\| > \rho}{\frac{1}{2}\langle \eta, J_{\theta^*} \eta\rangle} \), \( J_{\theta^*} \) being the matrix of \( D \)'s second derivatives at \( \theta^* \). This, clearly, is \( O(\rho^2) \).

The probability under \( \theta = 0 \) of seeing results \( X_n \) lying inside \( B_{\rho} \) is very different. If we've made \( \rho \) small enough that \( B_{\rho} \) doesn't include 0, \( \Probwrt{0}{X_n \in B_{\rho}} \rightarrow 0 \) exponentially fast, with rate \( \inf_{x \in B_{\rho}}{D_0(x)} \). Again, if \( \rho \) is small enough and \( D_0 \) is smooth enough, the value of the rate function should be essentially \( D_0(\theta^*) + O(\rho^2) \). If \( \theta^* \) in turn is close enough to 0 for a Taylor expansion, we'd get a rate of \( \frac{1}{2}\langle \theta^*, J_0 \theta^*\rangle \). To repeat, this is the exponential rate at which the p-value is going to zero when we test \( \theta=0 \) vs. \( \theta\neq 0 \), and the alternative value \( \theta^* \) is true. It is no accident that this is the same sort of rate we got for the simple Gaussian-mean problem.

Relating the matrix I'm calling \( J \) to the Fisher information matrix \( F \) needs a longer argument, which I'll present even more sketchily. The empirical distribution obeys a large deviations principle whose rate function is the Kullback-Leibler divergence, a.k.a. the relative entropy; this result is called "Sanov's theorem". For small perturbations of the parameter \( \theta \), the divergence between a distribution at \( \theta+\eta \) and that at \( \theta \) is, after yet another Taylor expansion and a little algebra, \( \langle \eta, F_{\theta} \eta \rangle \). A general result in large deviations theory, the "contraction principle", says that if the \( X_n \) obey an LDP with rate function \( D \), then \( Y_n = h(X_n) \) obeys an LDP with rate function \( D^{\prime}(y) = \inf_{x : h(x) = y}{D(x)} \). Thus an estimator which is a function of the empirical distribution, which is most of them, will have a decay rate which is at most \( \langle \eta, F_{\theta} \eta \rangle \), and possibly less, if it the estimator is crude enough. (The maximum likelihood estimator in an exponential family will, however, preserve large deviation rates, because it's a sufficient statistic.)

6. What's the Use of \( p \)-Values Then?

Much more limited than the bad old sort of research methods class (or third referee) would have you believe. If you find a small p-value, yay; you've got enough data, with precise enough measurement, to detect the effect you're looking for, or you're really unlucky. If your p-value is large, you're either really unlucky, or you don't have enough information (too few samples or too little precision), or the parameter is really close to zero. Getting a big p-value is not, by itself, very informative; even getting a small p-value has uncomfortable ambiguity. My advice would be to always supplement a p-value with a confidence set, which would help you tell apart "I can measure this parameter very precisely, and if it's not exactly 0 then it's at least very small" from "I have no idea what this parameter might be". Even if you've found a small p-value, I'd recommend looking at the confidence interval, since there's a difference between "this parameter is tiny, but really unlikely to be zero" and "I have no idea what this parameter might be, but can just barely rule out zero", and so on and so forth. Whether there are any scientific inferences you can draw from the p-value which you couldn't just as easily draw from the confidence set, I leave between you and your referees. What you definitely should not do is use the p-value as any kind of proxy for how important a parameter is.

If you want to know how much some variable matters for predictions of another variable, you are much better off just perturbing the first variable, plugging in to your model, and seeing how much the outcome changes. If you need a formal version of this, and don't have any particular size or distribution of perturbations in mind, then I strongly suggest using Gelman and Pardoe's "average predictive comparisons". If you want to know how much manipulating one variable will change another, then you're dealing with causal inference, but once you have a tolerable causal model, again you look at what happens when you perturb it. If what you really want to know is which variables you should include in your predictive model, the answer is the ones which actually help you predict, and this is why we have cross-validation (and have had it for as long as I've been alive), and, for the really cautious, completely separate validation sets. To get a sense of just how mis-leading p-values can be as a guide to which variables actually carry predictive information, I can hardly do better than Ward et al.'s "The Perils of Policy by p-Value", so I won't.

(I actually have a lot more use for p-values when doing goodness-of-fit testing, rather than as part of parametric estimation, though even there one has to carefully examine how the model fails to fit. But that's another story for another time.)

Nearly fifty years ago, R. R. Bahadur defined the efficiency of a test as the "rate at which it makes the null hypothesis more and more incredible as the sample size increases when a non-null distribution obtains", and gave a version of the large deviations argument to say that these rates should typically be exponential. The reason he could do so was that it was clear the p-value will always go to zero as we get more information, and so the issue is whether we're using that information effectively. In another fifty years, I presume that students will still have difficulties grasping this, but I piously hope that professionals will have absorbed the point.

References:

• R. R. Bahadur, "Rates of Convergence of Estimates and Test Statistics", Annals of Mathematical Statistics 38 (1967): 303--324
• R. R. Bahadur, Some Limit Theorems in Statistics (Philadelphia: Society for Industrial and Applied Mathematics, 1971)
• Andrew Gelman and Iain Pardoe, "Average Predictive Comparisons for Models with Nonlinearity, Interactions, and Variance Components", Sociological Methodology 37 (2007): 23--51 [PDF reprint via Andy]
• M. Stone, "Cross-Validatory Choice and Assessment of Statistical Predictions", Journal of the Royal Statistical Society B 36 (1974): 111--147
• Michael D. Ward, Brian D. Greenhill and Kristin M. Bakke, "The Perils of Policy by p-value: Predicting Civil Conficts", Journal of Peace Research 47 (2010): 363--375
• Aad van der Vaart, Asymptotic Statistics (Cambridge: Cambridge University Press, 1998)

*: For the sake of completeness, I should add that sometimes we need to replace the \( 1/n \) scaling by \( 1/r(n) \) for some increasing function \( r \), e.g., for dense graphs where \( n \) counts the number of nodes, \( r(n) \) would typically be \( O(n^2) \). ^

(Thanks to KLK for discussions, and feedback on a draft.)

Update, 17 May 2015: Fixed typos (backwards inequality sign, errant \( \theta \) for \( \rho \)) in large deviations section.

Manual trackback: Economist's View

Enigmas of Chance