Three-Toed Sloth

"Learning Spatio-Temporal Dynamics"

Attention conservation notice: Boasting about my student's just-completed doctoral dissertation. Over 2500 words extolling new statistical methods, plus mathematical symbols and ugly computer graphics, without any actual mathematical content, or even enough detail to let others in the field judge the results.

On Monday, my student Georg M. Goerg, last seen here leading Skynet to declare war on humanity at his dissertation proposal, defeated the snake — that is, defended his thesis:

Learning Spatio-Temporal Dynamics: Nonparametric Methods for Optimal Forecasting and Automated Pattern Discovery

Many important scientific and data-driven problems involve quantities that vary over space and time. Examples include functional magnetic resonance imaging (fMRI), climate data, or experimental studies in physics, chemistry, and biology.

Principal goals of many methods in statistics, machine learning, and signal processing are to use this data and i) extract informative structures and remove noisy, uninformative parts; ii) understand and reconstruct underlying spatio-temporal dynamics that govern these systems; and iii) forecast the data, i.e. describe the system in the future.

Being data-driven problems, it is important to have methods and algorithms that work well in practice for a wide range of spatio-temporal processes as well as various data types. In this thesis I present such generally applicable, statistical methods that address all three problems in a unifying approach.

I introduce two new techniques for optimal nonparametric forecasting of spatio-temporal data: hard and mixed LICORS (Light Cone Reconstruction of States). Hard LICORS is a consistent predictive state estimator and extends previous work from Shalizi (2003); Shalizi, Haslinger, Rouquier, Klinkner, and Moore (2006); Shalizi, Klinkner, and Haslinger (2004) to continuous-valued spatio-temporal fields. Mixed LICORS builds on a new, fully probabilistic model of light cones and predictive states mappings, and is an EM-like version of hard LICORS. Simulations show that it has much better finite sample properties than hard LICORS. I also propose a sparse variant of mixed LICORS, which improves out-of-sample forecasts even further.

Both methods can then be used to estimate local statistical complexity (LSC) (Shalizi, 2003), a fully automatic technique for pattern discovery in dynamical systems. Simulations and applications to fMRI data demonstrate that the proposed methods work well and give useful results in very general scientific settings.

Lastly, I made most methods publicly available as R (R Development Core Team, 2010) or Python (Van Rossum, 2003) packages, so researchers can use these methods and better understand, forecast, and discover patterns in the data they study.

PDF [7 Mb]

If you want to predict a spatio-temporal process, your best bet is to come up with an appropriately-detailed model of its dynamics, solve the model, estimate its parameters, and extrapolate it forward. Unfortunately, this is Real Science, and I gave up real science because it is hard. Coming up with a good mechanistic model of fluid flow, or combustion, or (have mercy) how the metabolic activity of computing neurons translates into blood flow and so into fMRI signals, is the sort of undertaking which could easily go on for years (or a century), and burning one graduate student per data set is wasteful. It would be nice to have a more automatic technique, which learns the dynamics from the data; at least, some representation of the dynamics. (We know this can be done for non-spatial dynamics.)

One might ignore the fact that the dynamics are spread out over space, and turn to modern time series methods. But this is not a good idea; even if the spatial extent is very modest, one is quickly dealing with very high-dimensional data, and the curse of dimensionality becomes crushing. Treating every spatial location as its own time series, and ignoring spatial dependence, is equally dubious. Now, just as there are unprincipled parametric statistical models of time series (ARMA et al.), there are unprincipled parametric statistical models of spatio-temporal data, but these offend me aesthetically, much as ARMA-mongering does. (I would sharply distinguish between these models, and parametric stochastic models which try to represent actual mechanisms.)

What Georg worked with in his thesis is the idea that, while spatial dependence matters, in spatio-temporal systems, it's generally not the case that every part of space-time depends on every other part of space-time. Suppose we want to predict what will happen at a particular point \( \vec{r} \) at a particular time \( t \). If influence can only propagate through the process at a finite speed \( c \), then recent events elsewhere can only matter if they are nearby spatially; for more spatially remote events to matter, they must be older. In symbols, what occured at another point-instant \( \vec{s},u \) could influence what happens at \( \vec{r},t \) only if \( \|\vec{s}-\vec{r}\| \leq c(t-u) \). Call this region of space-time the past cone of our favorite point-instant. Likewise, what happens at our point-instant can only influence those point-instants in its future cone, those where \( \|\vec{s}-\vec{r}\| \leq c(u-t) \).

I realize that such verbal-algebraic definitions are harder to follow than pictures, so I have prepared one. Take it away, T. rex:

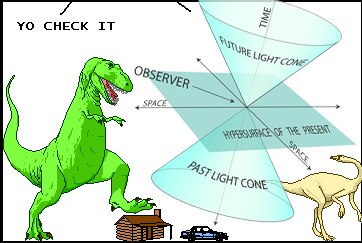
Of course the whole idea is ripped off from special relativity, and so has to apply when the data are measured at a high enough time resolution, but we don't really need that. So long as there is some finite speed of propagation, we can use that to define past and future cones⁰. The very nice consequence is that conditioning on the past cone screens off what happens at \( \vec{r}, t \) from what happens in the rest of space-time. This means that instead of having to predict the future of the whole spatial configuration from the past of the whole spatial configuration, we just need to predict the future at each point from its past cone. We've traded a single huge-dimensional problem for a lot of much-lower-dimensional problems, which is a big gain.

When we want to actually do this prediction at a given point, we want to know the distribution of the configuration in the future cone conditional on the contents of the past cone. Call this the "predictive distribution" for short. At this point, we could apply whatever predictive method we want. There is however one which has a nice connection to the idea of reconstructing the dynamics from the observed behavior. Suppose we had access to an Oracle which could tell us when two past-cone configurations would lead to the same predictive distribution. We would then, if we were not idiots, group together pasts which led to the same predictive distribution, and just remember, at each point-instant, which predictive distribution equivalence class we're dealing with. (We would pool data about actual futures within a class, and not across classes.) The class labels would be the minimal sufficient statistic for predicting the future. Since "predictive distribution equivalence class" is a mouthful, we'll call these predictive states, or, following the literature, causal states. Every point-instant in space-time gets its own predictive state, with nice strong Markov properties, and exactly the sort of screening-off you'd expect from a causal model, so the latter name isn't even a total stretch^1.

Since we do not have an Oracle, we try to approximate one, by building our own equivalence classes among histories. This amounts to clustering past cone configurations, based not on whether the configurations look similar, but whether they lead to similar predictive consequences. (We replace the original geometry in configuration-space by a new geometry in the space of predictive distributions, and cluster there.) In the older papers Georg mentioned in his abstract, this clustering was done in comparatively crude ways that only worked with discrete data, but it was always clear that was just a limitation of the statistical implementation, not the underlying mathematics. One could, and people like Jänicke et al. did, just quantize continuous data, but we wanted to avoid taking such a step.

For the original LICORS algorithm, Georg cracked the problem by using modern idea for high-dimensional testing. Basically, if we assume that the predictive state space isn't too rich, as we observe the process for longer and longer we gain more and more information about every configuration's predictive consequences, and grouping them together on the basis of statistical powerful hypothesis tests yields a closer and closer approximation to the true predictive states and their predictive distributions. (I won't go into details here; read the paper, or the dissertation.)

This is basically a "hard" clustering, and experience suggests that one often gets better predictive performance from "soft", probabilistic clustering². This is what "mixed LICORS" does --- it alternates between assigning each history to a fractional share in different predictive states, and re-estimating the states' predictive distributions. As is usual with non-parametric EM algorithms, proving anything is pretty hopeless, but it definitely works quite well.

To see how well, we made up a little spatio-temporal stochastic process, with just one spatial dimension. The observable process is non-Gaussian, non-Markovian, heteroskedastic, and, in these realizations, non-stationary. There is a latent state process, and, given the latent state, the observable process is conditionally Gaussian, with a variance of 1. (I won't give the exact specification, you can find it in the thesis.) Because there is only one spatial dimension, we can depict the whole of space and time in one picture, viewing the realization sub specie aeternitatis. Here is one such Spinoza's-eye-view of a particular realization, with time unrolling horizontally from left to right:

Since this is a simulation, we can work out the true predictive distribution. In fact, we rigged the simulation so that the true predictive distribution is always homoskedastic and Gaussian, and can be labeled by the predictive mean. For that realization, it looks like this:

LICORS of course doesn't know this; it doesn't know about the latent state process, or the parametric form of the model, or even that there is such a thing as a Gaussian distribution. All it gets is one realization of the observed process. Nonetheless, it goes ahead and constructs its own predictive states³. When we label those by their conditional means (even though we're really making distributional forecasts), we get this:

Qualitatively, this looks like we're doing a pretty good job of matching both the predictions and the spatio-temporal structure, even features which are really not obvious in the surface data. Quantitatively, we can compare how we're doing to other prediction methods:

Mean squared errors of different models, evaluated on independent realizations of the same process. "Mean per row" learns a different constant for each spatial location. The AR(p) models, of various orders, learn a separate linear autoregressive model for each spatial location. The VAR(p) models learn vector autoregressions for the whole spatial configuration, with Lasso penalties as in Song and Bickel. The "truth" is what an Oracle which knew the underlying model could achieve; the final columns show various tweaks to the LICORS algorithm.

In other words, hard LICORS predicts really well, starting from no knowledge of the dynamics, and mixed LICORS (not shown in that figure; read the dissertation!) is even stronger. Of course, this only works because the measurement resolution, in both space and time, is fine enough that there is a finite speed of propagation. If we reduced the time-resolution enough, every point could potentially influence every other in between each measurement, and the light-cone approach delivers no advantage. (At the other extreme, if there really is no spatial propagation of influence, the cones reduce to the histories of isolated points.) A small amount of un-accounted-for long-range connections doesn't seem to present large problems; being precise about that would be nice. So would implementing the theoretical possibility of replacing space with an arbitrary, but known, network.

Once we have a predictive state for each point-instant, we can calculate how many bits of information about the past cone configuration is needed to specify the predictive state. This is the local statistical complexity, which we can use for automatic filtering and pattern discovery. I wrote about that idea lo these many years ago, but Georg has some very nice results in his thesis on empirical applications of the notion, not just the abstract models of pattern formation I talked about. We can also use the predictive-state model to generate a new random field, which should have the same statistical properties as the original data, i.e., we can do a model-based bootstrap for spatio-temporal data, but that's really another story for another time.

Clearly, Georg no longer has anything to learn from me, so it's time for him to leave the ivory tower, and go seek his fortune in Manhattan. I am very proud; congratulations, Dr. Goerg!

0: When I mentioned this idea in Lyon in 2003, Prof. Vincenzo Capasso informed me that Kolmogorov used just such a construction in a 1938 paper modeling the crystallization of metals, apparently introducing the term "causal cone". Whether Kolmogorov drew the analogy with relativity, I don't know. ^

[1]: One discovery of this construction for time series was that of Crutchfield and Young, just linked to; similar ideas were expressed earlier by Peter Grassberger. Later independent discoveries include that of Jaeger, of Littman, Sutton and Singh, and of Langford, Salakhutdinov and Zhang. The most comprehensive set of results for one-dimensional stochastic processes is actually that of Knight from 1975. The earliest is from Wesley Salmon, in his Statistical Explanation and Statistical Relevance (1971). The information bottleneck is closely related, as are some of Lauritzen's ideas about sufficient statistics and prediction. I have probably missed other incarnations. ^

[2]: Obviously, that account of how mixed LICORS came about is a lie rational reconstruction. It really grew out of Georg's using an analogy with mixture models when trying to explain predictive states to neuroscientists. In a mixture model for \( Y \), we write \[ \Pr(Y=y) = \sum_{s}{\Pr(S=s)\Pr(Y=y|S=s)} \] where the sum is over the components or profiles or extremal distributions in the mixture. Conditioning on another variable, say \( X \) \[ Pr(Y=y|X=x) = \sum_{s}{\Pr(S=s|X=x)\Pr(Y=y|S=s,X=x)} \] which is clearly going to be even more of a mess than the marginal distribution. Unless, that is, \( \Pr(S=s|X=x) \) collapses into a delta function, which will happen when \( S \) is actually a statistic calculable from \( X \). The predictive states are then the profiles in a mixture model optimized for prediction. ^

[3]: LICORS needs to know the speed of propagation, \( c \), and how far the past and future cones should extend in time. If there are no substantive grounds for choosing these control settings, these can be set by cross-validation. There's not a lot of theory to back that up, but in practice it works really well. Getting some theory of cross-validation for this setting would be great. ^

Update, 29 December 2012: Small typo fixes and wording improvements.

Complexity; Enigmas of Chance; Kith and Kin