That Word Does Not Exist In Any Language
Attention conservation notice: 1500 words on a dispute at the intersection of paleography and computational linguistics, two areas in which I have no qualifications; also a sermon on a text from Lichtenberg: "We must not seek to abstract from the busts of the great Greeks and Romans rules for the visible form of genius as long as we cannot contrast them with Greek blockheads."
Over the weekend, I read Mark Liberman's post at Language Log about the new Rao et al. paper in Science, claiming to show information-theoretically that the symbols recovered on artifacts from the Harappan civilization in the Indus Valley are in fact a form of writing, as had long been supposed but was denied a few years ago by Farmer, Sproat and Witzel.
What Rao et al. claimed to show is that the sequences of Indus symbols possess information-theoretic properties which are distinctive of written language, as opposed to other symbols sequences, say ones which are completely random (IID, their "type 1 nonlinguistic") or completely deterministic (their "type 2 nonlinguistic"). Specifically, they examined the conditional entropy of sequence pairs (i.e., the entropy of the next symbol given the previous one). The claim is that the Indus symbols have the same pattern for their conditional entropy as writing systems, which is clearly distinguishable from non-linguistic symbol sequences by these means.
As someone who is very, very into information theory (especially conditional entropy), I was intrigued, but also very puzzled by Mark's account, from which it seemed that Rao et al. had a huge gap where the core of their paper should be. Actually reading the paper convinced me that Mark's account was correct, and there was a huge logical fallacy. I'll reproduce Figure 1A from the paper and explain what I mean.
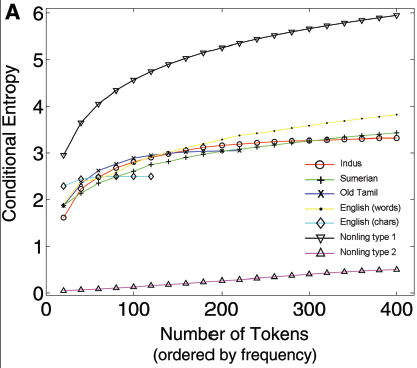
Rao et al. worked with a corpus of Indus Valley inscriptions, which recognizes 417 distinct symbol types. This is their "Indus" line. The other language lines come from different corpora in the indicated language. In each corpus, they filtered out the less common symbols, and then fit a first-order Markov chain. (Transition probabilities were estimated with a smoothing estimator rather than straight maximum likelihood.) Then they calculated the conditional entropy of the chain, using the estimated transition probabilities and the observed symbol frequencies (rather than say the invariant distribution of the chain); that's the vertical axis. The horizontal axis shows how many symbol types were retained --- i.e., "100 tokens" means that only the 100 most common symbols in the corpus were kept, and the chain was fit to those sequences. (This is not explained in the paper but was made clear in later correspondence between Sproat and the authors.) There are two lines for English, depending on whether "token" was taken to mean "character" (differentiating upper and lower case) or to mean "word".
The bottom curve shows the estimated conditional entropy from a purely deterministic sequence; the actual conditional entropy is in fact zero, so I presume that the upward trend is an artifact of the smoothed transition probabilities. The top curve, on the other hand, is from a uniform IID sequence --- here the real conditional entropy is the same as the marginal entropy, but both grow as N increases because the size of the symbol set grows. (I.e., this is an artifact of keeping only the most common symbols.)
Here is the flaw: there is no demonstration that only linguistic sequences have this pattern in their conditional entropies. Rao et al. have shown that two really extreme non-linguistic processes don't, but that's not a proof or even a plausibility argument. I would settle for an argument that non-linguistic processes have to be really weird to show this pattern, but even that is lacking. In Mayo's terms, they have not shown that this test has any severity.
Of course the fact that they haven't shown their test is severe doesn't mean that it isn't, in fact, severe. So, by way of procrastinating, I spent some time yesterday constructing a counter-example. My starting point was what Mark had done, generating a sequence of IID draws from a geometric distribution (rather than a uniform one) and subjecting it to the same analysis as Rao et al. As it happens, I had already written a function in R to fit Markov chains and calculate their log-likelihood, and here the conditional entropy is the negative log likelihood over the sequence length. (Admittedly this is only true using the maximum likelihood estimates for transition probabilities, rather than smoothed estimates as Rao et al. do, but my simulations had so much data this shouldn't matter.) Setting the rate of the geometric distribution to 0.075, here were my first results.
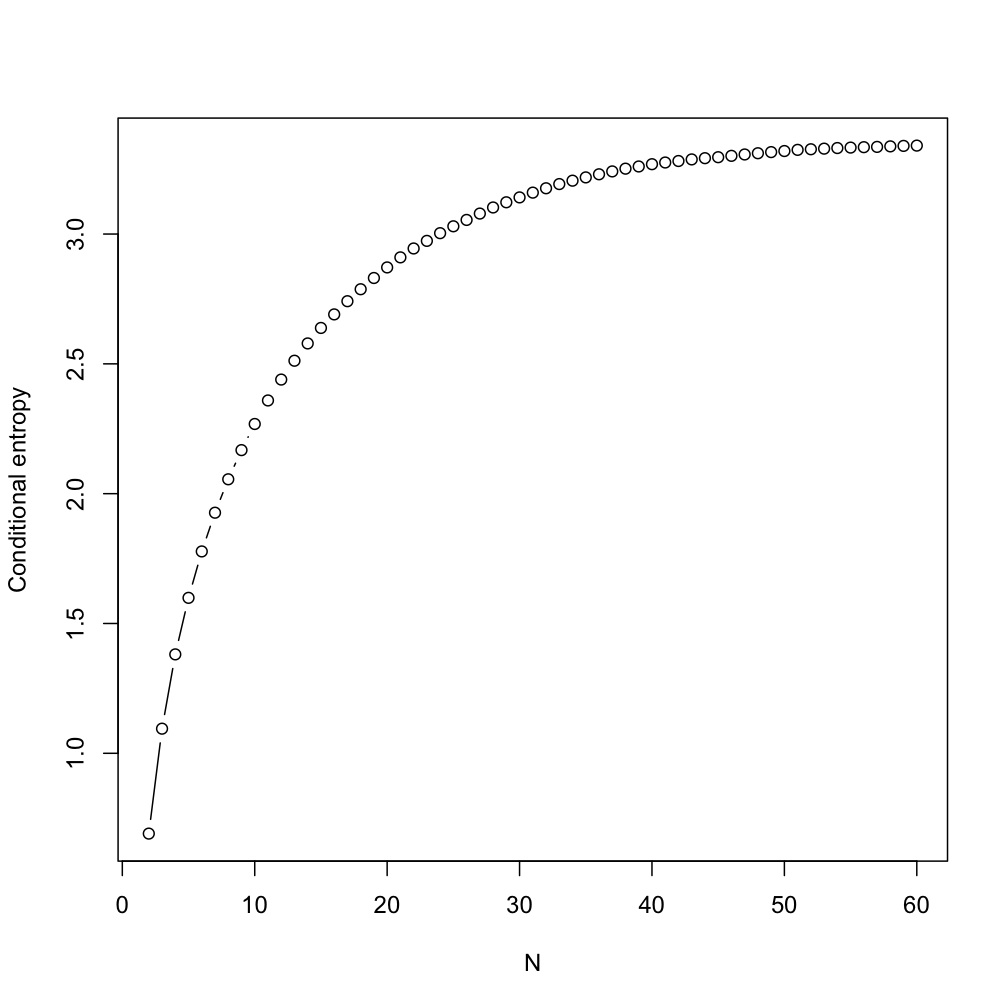
Mark Liberman and Richard Sproat did almost the same thing pretty much simultaneously, as you can see from the updates to Mark's post.
This was not entirely satisfactory, since (as Rao et al. point out in the online supplementary materials), there is a big gap between the marginal and conditional entropies for writing and for the Indus symbols. This was also, however, not too hard to finesse. In addition to the geometric sequence, I generated a Markov chain which alternated between the values +1 and -1, but where each positive or negative sign was 99% likely to be followed by the same sign. (That is, the signs were highly persistent.) I then multiplied the IID geometric variables (plus 1) by the Markov signs. This gave a larger set of symbols, but where knowing the sign of the current symbol (which "register" or "sub-vocabulary" it came from) was quite informative about the sign of the next symbol. (I added 1 to the geometric variables to exclude 0=-0, keeping the sub-vocabularies distinct.)
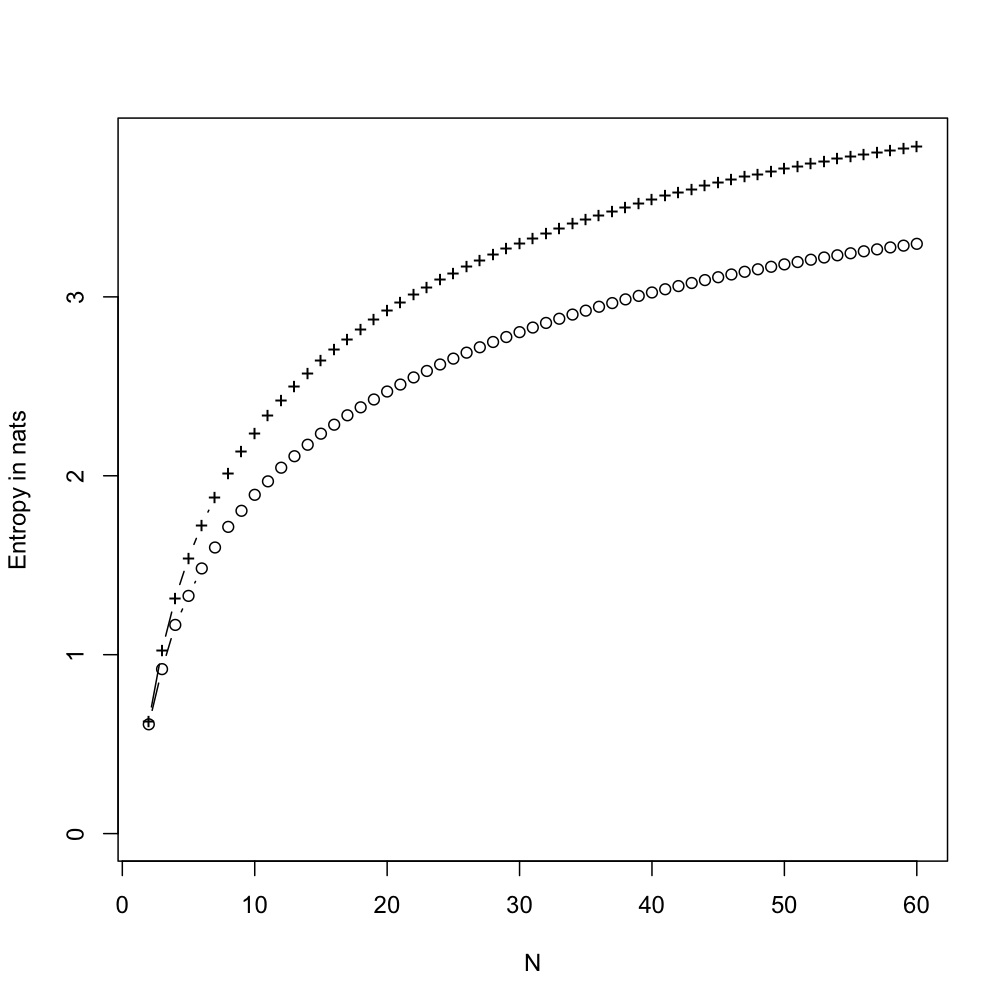
Pluses: marginal entropy; circles: conditional entropy
A third experiment takes after the fact that the Indus symbol sequences are all extremely short, at most a dozen characters or so. In stead of having a Markov chain for the sign, I used another, independent set of random draws, uniform on the integers from 2 to 6, to divide the sequence into blocks, and gave all the symbols in each block the same (coin-toss) sign.
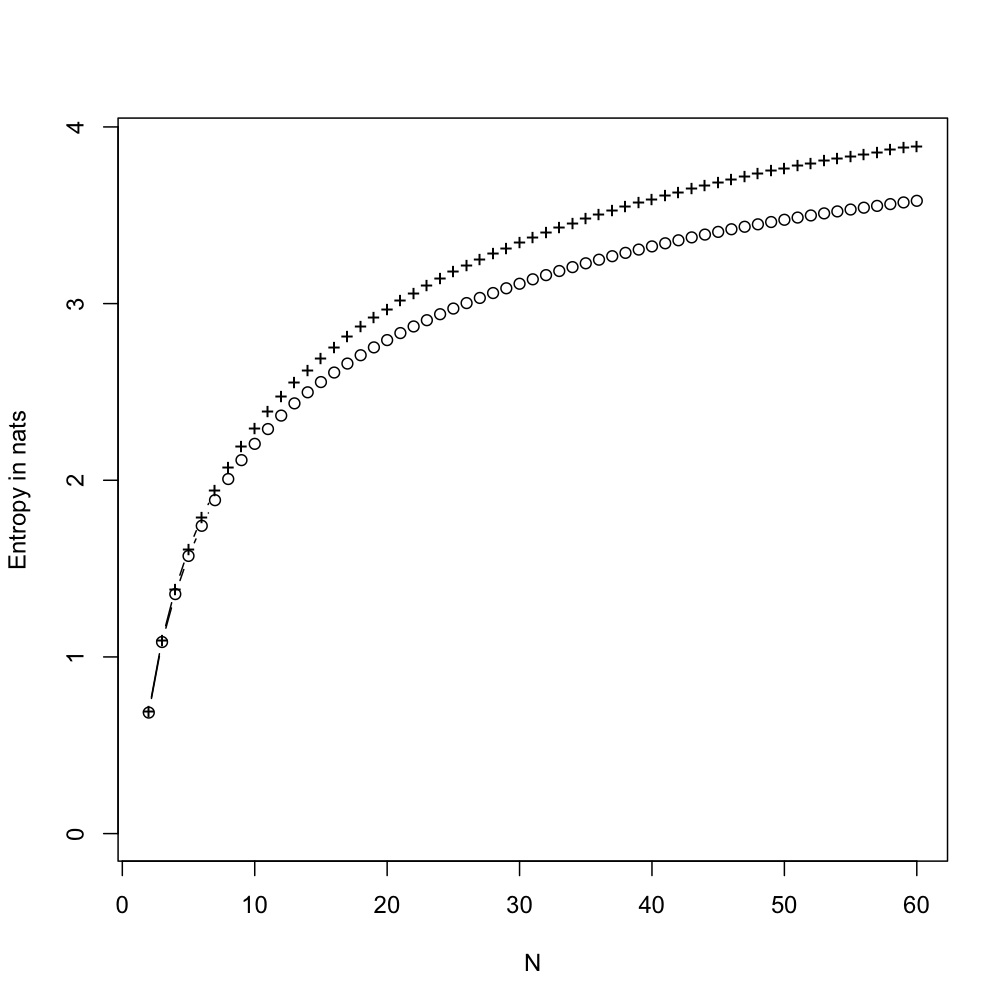
Pluses: marginal entropy; circles: conditional entropy
(Because I'm doing everything with a single long sequence, I artificially introduce transitions from positive to negative signs, which lowers the gap between the conditional and unconditional entropies. If I wanted to do this properly, I'd re-write my Markov estimator so it used many short sequences; but that would be too much like real work.)
The mechanism producing the gap between conditional and unconditional entropies is that the marginal distribution of symbols is a mixture of several pure distributions, and which mixture component we draw from now influences which component we'll draw from next (so the sequence can be Markov, exchangeable, etc.). Given the mixture components, the symbols are independent and the conditional and unconditional entropies are equal. Without that knowledge, the first symbol in effect is a cue for figuring out the mixture component, reducing the entropy of the second. There is nothing specifically linguistic about this; any hidden Markov model does as much. It would, for instance, work if the "symbols" were characters in randomly-selected comic books, who cluster (though slightly imperfectly); if that's too low-brow, think about Renaissance paintings, and the odds of seeing St. John the Baptist as opposed to a swan in one which contains Leda.
I have made no attempt to match the quantitative details Rao et al. report for the Indus symbols, just the qualitative patterns. Were I to set out seriously to do so, I'd get rid of the geometric distribution, and instead use a hidden Markov model with more than two states, each state having a distinct output alphabet, the distribution of which would be a Zipf (as used by Liberman or Sproat) or a Yule-Simon. (I might also try block-exchangeable sequences, as in my third example.) But this would approach real work, rather than a few hours of procrastination, and I think the point is made. Perhaps the specific results Rao et al. report can only be replicated by making distributional assumptions which are very implausible for anything except language, but I'd say that the burden of proof is on them. If, for instance, they analyzed lots of real-world non-linguistic symbol systems (like my comic books) and showed that all of them had very different conditional entropy curves than did actual writing, that would be a start.
I should in the interest of full disclosure say that a number of years ago Farmer and I corresponded about his work on the development of pre-modern cosmologies, which I find interesting and plausible (though very conjectural). But if anything I hope Farmer et al. are wrong and the Indus Valley civilization was literate, and I'd be extra pleased if the language were related to Tamil. Unfortunately, if that's the case it will need to be shown some other way, because these conditional entropy calculations have, so far as I can see, no relevance to the question at all.
My code (in R) is here if you want to play with this, or check if I'm doing something stupid. In the unlikely event you want more, I suggest reading the reply of Farmer et al., Rahul Siddharthan (especially the comments), or Fernando Pereira; the last is probably the wisest.
Manual trackback: Metadatta; Language Hat
Posted by crshalizi at April 28, 2009 22:30 | permanent link
![\[
f_n(\theta) = \sum_{k=0}^{n}{{n \choose k} \theta^k {(1-\theta)}^{n-k} \log{k!}}
\]](../sloth/604_1.gif)
![$ \mathbb{E}[\log{X!}] $](../sloth/604_2.gif) when X is binomially distributed?
when X is binomially distributed?

