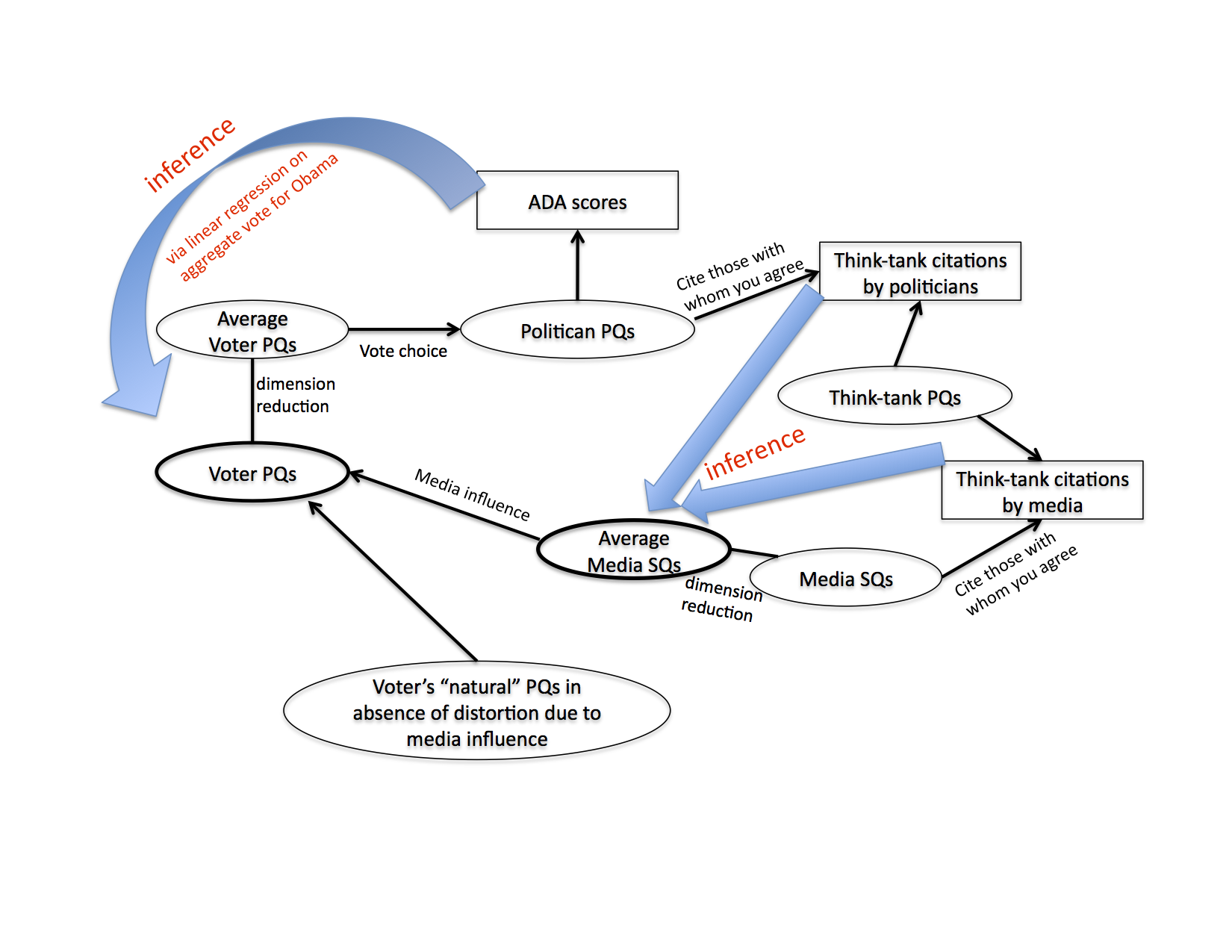
Cognitive Democracy
Attention conservation notice: 8000+ words of political
theory by geeks.
For quite a while now, Henry
Farrell and I have been worrying at a skein of ideas running between
institutions, networks,
evolutionary
games, democracy, collective
cognition, the Internet and inequality. Turning these threads into a
single seamless garment is beyond our hopes (and not our style anyway), but we
think we've been getting somewhere in at least usefully disentangling them. An
upcoming workshop gave us an excuse to set out part (but not all) of the
pattern, and so here's a draft. To the extent you like it, thank Henry; the
remaining snarls are my fault.
This is a draft, and anyway it's part of the spirit of the piece
that feedback would be appropriate. I do not have comments, for
my usual
reasons, but
it's cross-posted
at Crooked Timber
and The
Monkey Cage, and you can always send an e-mail.
(Very Constant Readers will now see the context for a lot of my
non-statistical writing over the last few years, including the previous post.)
Cognitive Democracy
Henry Farrell (George Washington University) and Cosma Rohilla Shalizi (Carnegie Mellon University/The Santa Fe Institute)
In this essay, we outline a cognitive approach to democracy. Specifically, we argue that democracy has unique benefits as a form of collective problem solving in that it potentially allows people with highly diverse perspectives to come together in order collectively to solve problems. Democracy can do this better than either markets and hierarchies, because it brings these diverse perceptions into direct contact with each other, allowing forms of learning that are unlikely either through the price mechanism of markets or the hierarchical arrangements of bureaucracy. Furthermore, democracy can, by experimenting, take advantage of novel forms of collective cognition that are facilitated by new media.
Much of what we say is synthetic --- our normative arguments build on both
the academic literature (Joshua Cohen's
and Josiah Ober's
arguments about epistemic
democracy; Jack Knight and James
Johnson's pragmatist account of the benefits of a radically egalitarian
democracy and Elster
and Landemore's
forthcoming collection on Collective Wisdom), and on arguments by
public intellectuals such
as Steven Berlin Johnson,
Clay Shirky, Tom Slee and Chris Hayes. We also seek to contribute to new
debates on the sources of collective wisdom. Throughout, we emphasize
the cognitive benefits of democracy, building on important results
from cognitive science, from sociology, from machine learning and from network
theory.
We start by explaining social institutions should do. Next, we examine sophisticated arguments that have been made in defense of markets (Hayek's theories about catallaxy) and hierarchy (Richard Thaler and Cass Sunstein's "libertarian paternalism") and discuss their inadequacies. The subsequent section lays out our arguments in favor of democracy, illustrating how democratic procedures have cognitive benefits that other social forms do not. The penultimate section discusses how democracy can learn from new forms of collective consensus formation on the Internet, treating these forms not as ideals to be approximated, but as imperfect experiments, whose successes and failures can teach us about the conditions for better decision making; this is part of a broader agenda for cross-disciplinary research involving computer scientists and democratic theorists.
Justifying Social Institutions
What are broad macro-institutions such as politics, markets and hierarchies
good for? Different theorists have given very different answers to this
question. The dominant tradition in political theory tends to evaluate them in
terms of justice --- whether institutions use procedures, or give
results, that can be seen as just according to some reasonable normative
criterion. Others, perhaps more cynically, have focused on their potential
contribution to stability --- whether they produce an acceptable level
of social order, which minimizes violence and provides some modicum of
predictability. In this essay, we analyze these institutions according to a
different criterion. We start with a pragmatist question - whether these
institutions are useful in helping us to solve difficult social
problems.
Some of the problems that we face in politics are simple ones (not in the
sense that solutions are easy, but in the sense that they are simple to
analyze). However, the most vexing problems are usually ones without any very
obvious solutions. How do we change legal rules and social norms in order to
mitigate the problems of global warming? How do we regulate financial markets
so as to minimize the risk of new crises emerging, and limit the harm of those
that happen? How do we best encourage the spread of human rights
internationally?
These problems are pressing --- yet they are difficult to think about
systematically, let alone solve. They all share two important features. First,
they are all social problems. That is, they are problems which involve
the interaction of large numbers of human beings, with different interests,
desires, needs and perspectives. Second, as a result, they are complex
problems, in the sense that scholars of complexity understand the term. To
borrow Scott Page's (2011, p. 25) definition, they involve "diverse
entities that interact in a network or contact
structure."
They are a result of behavior that is difficult to predict, so that
consequences to changing behavior are extremely hard to map out in
advance. Finding solutions is difficult, and even when we find one, it is hard
to know whether it is good in comparison to other possible solutions, let alone
the best.
We argue that macro-institutions will best be able to tackle these problems
if they have two features. First, they should foster a high degree of
direct communication between individuals with diverse viewpoints. This
kind of intellectual diversity is crucial to identifying good solutions to
complex problems. Second, we argue that they should provide relative
equality among affected actors in decision-making processes, so as to
prevent socially or politically powerful groups from blocking socially
beneficial changes to the detriment of their own particular interests.
We base these contentions on two sets of arguments, one from work on
collective problem solving, the other from theories of political power. Both
are clarified if we think of the possible solutions to a difficult problem as
points on a landscape, where we seek the highest point. Difficult problems
present many peaks, solutions that are better than the points close to
them. Such landscapes are rugged --- they have some degree of
organization, but are not so structured that simple algorithms can quickly find
the best solution. There is no guarantee that any particular peak
is globally optimal (i.e. the best solution across the entire
landscape) rather than locally optimal (the best solution within a
smaller subset of the landscape).
Solving a complex problem involves a search across this landscape for the
best visible solutions. Individual agents have limited cognitive abilities, and
(usually) limited knowledge of the landscape. Both of these make them likely to
get stuck at local optima, which may be much worse than even other local peaks,
let alone the global optimum. Less abstractly, people may settle for bad
solutions, because they do not know better (they cannot perceive other, better
solutions), or because they have difficulty in reaching these solutions
(e.g. because of coordination problems, or because of the ability of powerful
actors to veto possible changes).
Lu Hong and Scott Page (2004) use mathematical models to
argue that diversity of viewpoints helps groups find better
solutions (higher peaks on the landscape). The intuition is that different
individuals, when confronting a problem, "see" different landscapes --- they
organize the set of possible solutions in different ways, some of which are
useful in identifying good peaks, some of which less so. Very smart individuals
(those with many mental tools) have better organized landscapes than less smart
individuals, and so are less likely to get trapped at inferior local
optima. However, at the group level, diversity of viewpoints matters a
lot. Page and Hong find that "diversity trumps ability". Groups with high
diversity of internal viewpoints are better able to identify optima than groups
composed of much smarter individuals with more homogenous viewpoints. By
putting their diverse views together, the former are able to map out more of
the landscape and identify possible solutions that would be invisible to groups
of individuals with more similar perspectives.
Page and Hong do not model the social processes through which individuals
can bring their diverse points of view together into a common
framework. However, their arguments surely suggest that actors' different
points of view need to be exposed directly to each other, in order to
identify the benefits and drawbacks of different points of view, the ways in
which viewpoints can be combined to better advantage, and so on. These
arguments are supported by a plethora of work in sociology and elsewhere (Burt,
Rossman etc). As we explain at length below, some degree of clumping is also
beneficial, so so that individuals with divergent viewpoints do not converge
too quickly.
The second issue for collective problem solving is more obvious. Even when
groups are able to identify good solutions (relatively high peaks in the
solution landscape), they may not be able to reach them. In particular, actors
who benefit from the status quo (or who would prefer less generally-beneficial
solutions) may be able to use political and social power to block movement
towards such peaks, and instead compel movement towards solutions that have
lower social and greater individual benefits. Research on problem solving
typically does not talk about differences in actors' interests, or in actors'
ability successfully to pursue their interests. While different individuals
initially perceive different aspects of the landscape, researchers assume that
once they are able to communicate with each other, they will all agree on how
to rank visible solutions from best to worst. But actors may have diverse
interests as well as diverse understandings of the world (and the two may
indeed be systematically linked). They may even be working in such different
landscapes, in terms of personal advantage, that one actor's peak is another's
valley, and vice versa. Moreover, actors may differ in their ability to ensure
that their interests are prosecuted. Recent work in political theory (Knight
1992, Johnson and Knight 2011), economics (Bowles and Naidu, 2008), political
science (Hacker and Pierson 2010) and sociology details how powerful actors may
be able to compel weaker ones to accept solutions that are to the advantage of
the former, but that have lower overall social benefits.
Here, relative equality of power can have important
consequences. Individuals in settings with relatively equal power relations,
are, ceteris paribus more likely to converge on solutions with broad
social benefits, and less likely to converge on solutions that benefit smaller
groups of individuals at the expense of the majority. Furthermore, equal power
relations may not only make it easier to converge on "good" solutions when they
have been identified, but may stimulate the process of search for such
solutions. Participating in the search for solutions and in decision-making
demands resources (at a minimum, time), and if those resources are concentrated
in a small set of actors, with similar interests and perspectives, the
solutions they will find will be fewer and worse than if a wide variety of
actors can also search.
With this in mind, we ask whether different macro-institutions are better,
or worse at solving the complex problems that confront modern economies and
societies. Institutions will tend to do better to the extent that they both (i)
bring together people with different perspectives, and (ii) share
decision-making power relatively equally. Our arguments are, obviously, quite
broad. We do not speak much to the specifics of how macro-institutions work,
instead focusing on the broad logics of these different
macro-institutions. Furthermore, we do not look at the ways in which our
desiderata interact with other reasonable desiderata (such as social stability,
justice and so on). Even so, we think that it is worth clarifying the ways in
which different institutions can, or cannot, solve complex problems. In recent
decades, for example, many scholars and policy makers have devoted time and
energy to advocating markets as the way to address social problems
that are too complex to be solved by top-down authority. As we show below,
markets, to the extent that they imply substantial power inequalities, and
increasingly homogenize human relations, are unlikely to possess the virtues
attributed to them, though they can have more particular benefits under
specific circumstances. Similarly, hierarchy suffers from dramatic
informational flaws. This prompts us to reconsider democracy, not for the sake
of justice or stability, but as a tool for solving the complex problems faced
by modern societies.
Markets and Hierarchies as Ways to Solve Complex Problems
Many scholars and public intellectuals believe that markets or hierarchies
provide better ways to solve complex problems than democracy. Advocates of
markets usually build on the groundbreaking work of F. A. von Hayek, to argue
that market based forms of organization do a better job of eliciting
information and putting it to good work than does collective
organization. Advocates of hierarchy do not write from any such unified
tradition. However, Richard Thaler and Cass Sunstein have recently made a
sophisticated case for the benefits of hierarchy. They advocate a combination
of top-down mechanism design and institutions designed to guide choices rather
than to constrain them - what they call libertarian paternalism - as a way to
solve difficult social problems. Hayek's arguments are not the only case for
markets, and Thaler and Sunstein's are not the only justification for
hierarchy. They are, however, among the best such arguments, and hence
provide a good initial way to test the respective benefits of markets,
hierarchies and democracies in solving complex problems. If there are better
arguments, which do not fall victim to the kinds of problems we point to, we
are not aware of them (but would be very happy to be told of them).
Hayek's account of the informational benefits of markets is
groundbreaking. Although it builds on the insights of others (particularly
Michael Polanyi), it is arguably the first real effort to analyze how social
institutions work as information-processors. Hayek reasons as follows. Much of
human knowledge (as Polanyi argues) is practical, and cannot be fully
articulated ("tacit"). This knowledge is nonetheless crucial to economic
life. Hence, if we are to allocate resources well, we must somehow gather this
dispersed, fragmentary, informal knowledge, and make it useful.
Hayek is explicit that no one person can know all that is required to
allocate resources properly, so there must be a social mechanism for
such information processing. Hayek identifies three possible mechanisms:
central planning, planning by monopolistic industries, and decentralized
planning by individuals. He argues that the first and second of these break
down when we take account of the vast amount of tacit knowledge, which cannot
be conveyed to any centralized authority. Centralized or semi-centralized
planning are especially poor at dealing with the constant flows of major and
minor changes through which an economy (or, as Hayek would prefer, a catallaxy)
approaches balance. To deal with such changes, we need people to make the
necessary decisions on the spot --- but we also need some way to convey the
appropriate information about changes in the larger economic system to him or
her. The virtue of the price system, for Hayek, is to compress diffuse, even
tacit, knowledge about specific changes in specific circumstances into a single
index, which can guide individuals as to how they ought respond to changes
elsewhere. I do not need to grasp the intimate local knowledge of the farmer
who sells me tomatoes in order to decide whether to buy their products. The
farmer needs to know the price of fertilizer, not how it is made, or what it
could be used for other than tomatoes, or the other uses of the fertilizers'
ingredients. (I do not even need to know the price of fertilizer.) The
information that we need, to decide whether to buy tomatoes or to buy
fertilizer, is conveyed through prices, which may go up or down, depending on
the aggregate action of many buyers or suppliers, each working with her own
tacit understandings.
This insight is both crucial and beautiful, yet it has stark limits. It
suggests that markets will be best at conveying a particular kind of
information about a particular kind of underlying facts, i.e., the relative
scarcity of different goods. As Stiglitz (2000) argues, market signals about
relative scarcity are always distorted, because prices embed information about
many other economically important factors. More importantly, although
information about relative scarcity surely helps markets approach some kind of
balance, it is little help in solving more complicated social problems, which
may depend not on allocating existing stocks of goods in a useful way, given
people's dispersed local knowledge, so much as discovering new goods or new
forms of allocation. More generally, Hayek's well-known detestation for
projects with collective goals lead him systematically to discount the ways in
which aggregate knowledge might work to solve collective rather than individual
problems.
This is unfortunate. To the extent that markets fulfil Hayek's criteria, and
mediate all relevant interactions through the price mechanism, they foreclose
other forms of exchange that are more intellectually fruitful. In particular,
Hayek's reliance on arguments about inarticulable tacit knowledge mean that he
leaves no place for reasoned discourse or the useful exchange of views. In
Hayek's markets, people communicate only through prices. The advantage of
prices, for Hayek, is that they inform individuals about what others want (or
don't want), without requiring anyone to know anything about anyone else's
plans or understandings. But there are many useful forms of knowledge that
cannot readily be conveyed in this way.
Individuals may learn something about those understandings as
a by-product of market interactions. In John Stuart Mill's
description:
But the economical advantages of commerce are surpassed in importance by
those of its effects which are intellectual and moral. It is hardly possible to
overrate the value, in the present low state of human improvement, of placing
human beings in contact with persons dissimilar to themselves, and with modes
of thought and action unlike those with which they are familiar. Commerce is
now what war once was, the principal source of this contact.
However, such contact is largely incidental --- people engage in market
activities to buy or to sell to best advantage, not to learn. As markets become
purer, in both the Hayekian and neo-classical senses, they produce ever less of
the contact between different modes of life that Mill regards as salutary. The
resurgence of globalization; the creation of an Internet where people who will
only ever know each other by their account names buy and sell from each other;
the replacement of local understandings with global standards; all these
provide enormous efficiency gains and allow information about supply and demand
to flow more smoothly. Yet each of them undermines the Millian benefits of
commerce, by making it less likely that individuals with different points of
view will have those perspectives directly exposed to each other. More
tentatively, markets may themselves have a homogenizing impact on differences
between individuals and across societies, again reducing diversity. As Albert
Hirschman shows, there is a rich, if not unambiguous, literature on the global
consequences of market society. Sociologists such as John Meyer and his
colleagues find evidence of increased cultural and social convergence across
different national contexts, as a result of exposure to common market and
political forces.
In addition, it is unclear whether markets in general reduce power
inequalities or reinforce them in modern democracies. It is almost certainly
true that the spread of markets helped undermine some historical forms of
hierarchy, such as feudalism (Marx). It is not clear that they
continue to do so in modern democracies. On the one hand, free market
participation provides individuals with some ability (presuming equal market
access, etc.) to break away from abusive relationships. On the other, markets
provide greater voice and choice to those with more money; if money talks in
politics, it shouts across the agora. Nor are these effects limited to the
marketplace. The market facilitates and fosters asymmetries of wealth which in
turn may be directly or indirectly translated into asymmetries of political
influence (Lindblom). Untrammeled markets are associated with gross income
inequalities, which in turn infects politics with a variety of
pathologies. This suggests that markets fail in the broader task of exposing
individuals' differing perspectives to each to each other. Furthermore, markets
are at best indifferent levelers of unequal power relations.
Does hierarchy do better? In an influential recent book, Richard Thaler and
Cass Sunstein suggest that it does. They argue that "choice architects", people
who have "responsibility for organizing the context in which people make
decisions," can design institutions so as to spur people to take better choices
rather than worse ones. Thaler and Sunstein are self-consciously paternalist,
claiming that flawed behavior and thinking consistently stop people from making
the choices that are in their best interests. However, they also find direct
control of people's choices morally opprobrious. Libertarian paternalism seeks
to guide but not eliminate choice, so that the easiest option is the "best"
choice that individuals would make, if they only had sufficient
attention and discipline. It provides paternalistic guidance through
libertarian means, shaping choice contexts to make it more likely that
individuals will make the right choices rather than the wrong ones.
This is, in Thaler and Sunstein's words, a politics of "nudging" choices
rather than dictating them. Although Thaler and Sunstein do not put it this
way, it is also a plea for the benefits of hierarchy in organizations and, in
particular, in government. Thaler and Sunstein's "choice architects" are
hierarchical superiors, specifically empowered to create broad schemes that
will shape the choices of many other individuals. Their power to do this does
not flow from, e.g., accountability to those whose choices get shaped. Instead,
it flows from positions of authority within firm or government, which allow
them to craft pension contribution schemes within firms, environmental policy
within the government, and so on.
Thaler and Sunstein's recommendations have outraged libertarians, who
believe that a nudge is merely a well-aimed shove --- that individuals' freedom
will be reduced nearly as much by Thaler and Sunstein's choice architecture, as
it would be by direct coercion. We are also unenthusiastic
about libertarian paternalism, but for different reasons. While we do not
talk, here, about coercion, we have no particular normative objection to it,
provided that it is proportionate, directed towards legitimate ends, and
constrained by well-functioning democratic controls. Instead, we worry that the
kinds of hierarchy that Thaler and Sunstein presume actively inhibit the
unconstrained exchange of views that we see as essential to solving complex
problems.
Bureaucratic hierarchy is an extraordinary political achievement. States
with clear, accountable hierarchies can achieve vast and intricate projects,
and businesses use hierarchies to coordinate highly complex chains of
production and distribution. Even so, there are reasons why bureaucracies have few
modern defenders. Hierarchies rely on power asymmetries to work. Inferiors take
orders from superiors, in a chain of command leading up to the chief executive
officer (in firms) or some appointed or non-appointed political actor (in
government). This is good for pushing orders down the chain, but
notoriously poor at transmitting useful information up, especially
kinds of information superiors did not anticipate wanting. As scholars from Max
Weber on have emphasized, bureaucracies systematically encourage a culture of
conformity in order to increase predictability and static efficiency.
Thaler and Sunstein presume a hierarchy in which orders are followed and
policies are implemented, but ignore what this implies about feedback. They
imagine hierarchically-empowered architects shaping the choices of a less
well-informed and less rational general population. They discuss ordinary
people's bad choices at length. However, they have remarkably little to say
about how it is that the architects housed atop the hierarchy can figure out
better choices on these individuals' behalf, or how the architectures can
actually design choice systems that will encourage these choices. Sometimes,
Thaler and Sunstein suggest that choice architects can rely on introspection:
"Libertarian paternalists would like to set the default by asking what
reflective employees in Janet's position would actually want." At other times,
they imply that choice architects can use experimental techniques. The book's
opening analogy proposes a set of experiments, in which the director of food
services for a system "with hundreds of schools" (p. 1), "who likes to think
about things in non-traditional ways," experiments with different arrangements
of food in order to discover which displays encourage kids to pick the
healthier options. Finally, Thaler and Sunstein sometimes argue that choice
architects can use results from the social sciences to find optima.
One mechanism of information gathering that they systematically ignore is
active feedback from citizens. Although they argue in passing that feedback
from choice architects can help guide consumers, e.g., giving
information about the content of food, or by shaping online interactions to
ensure that people are exposed to others' points of view, they have no place
for feedback from the individuals whose choices are being manipulated to help
guide the choice architects, let alone to constrain them. As Suzanne Mettler
(2011) has pointed out, Thaler and Sunstein depict citizens as passive
consumers, who need to be guided to the desired outcomes, rather than active
participants in democratic decision making.
This also means that Thaler and Sunstein's proposals don't take advantage of
diversity. Choice architects, located within hierarchies which tend generically
to promote conformity, are likely to have a much more limited range of ways of
understanding problems than the population whose choices they are seeking to
structure. In Scott Page's terms, these actors are may very "able" --- they
will have sophisticated and complex heuristics, so that each individual choice
architect is better able than each individual member of the population to see a
large portion of the landscape of possible choices and outcomes. However, the
architects will be very similar to each other in background and training, so
that as a group they will see a far more limited set of possibilities
than a group of randomly selected members of the population (who are likely to
have less sophisticated but far more diverse heuristics). Cultural homogeneity
among hierarchical elites helps create policy disasters (the "best and
brightest" problem). Direct involvement of a wider selection of actors with
more diverse heuristics would alleviate this problem.
However, precisely because choice architects rely on hierarchical power to
create their architectures, they will have difficulty in eliciting feedback,
even if they want to. Inequalities of power notoriously dampen real exchanges
of viewpoints. Hierarchical inferiors within organizations worry about
contradicting their bosses. Ordinary members of the public are uncomfortable
when asked to contradict experts or officials. Work on group decision making
(including, e.g., Sunstein 2003) is full of examples of how perceived power
inequalities lead less powerful actors either to remain silent, or merely to
affirm the views of more powerful actors, even when they have independently
valuable perspectives or knowledge.
In short, libertarian paternalism is flawed, not because it restricts
peoples' choices, but because it makes heroic assumptions about choice
architects' ability to figure out what the actual default choices should be,
and blocks their channels for learning better. Choice architects will be likely
to share a narrow range of sophisticated heuristics, and to have difficulty in
soliciting feedback from others with more diverse heuristics, because of their
hierarchical superiority and the unequal power relations that this
entails. Libertarian paternalism may still have value in situations of
individual choice, where people likely do "want" e.g. to save more or take more
exercise, but face commitment problems, or when other actors have an incentive
to misinform these people or to structure their choices in perverse ways in the
absence of a 'good' default choice. However, it will be far less useful, or
even actively pernicious, in complex situations, where many actors with
different interests make interdependent choices. Indeed, Thaler and Sunstein
are far more convincing when they discuss how to encourage people to choose
appropriate pension schemes than when they suggest that environmental problems
are the "outcome of a global choice architecture system" that could be usefully
rejiggered via a variety of voluntaristic mechanisms.
Democracy as a way to solve complex problems
Is democracy better at identifying solutions to complex problems? Many ---
even on the left --- doubt that it is. They point to problems of finding common
ground and of partisanship, and despair of finding answers to hard
questions. The dominant tradition of American liberalism actually has
considerable distaste for the less genteel aspects of democracy. The early 20th
century Progressives and their modern heirs deplore partisanship and political
rivalry, instead preferring technocracy, moderation and deliberation (Rosenblum
2008). Some liberals (e.g., Thaler and Sunstein) are attracted to Hayekian
arguments for markets and libertarian paternalist arguments for hierarchy
exactly because they seem better than the partisan rancor of democratic
competition.
We believe that they are wrong, and democracy offers a better way of solving
complex problems. Since, as we've argued, power asymmetries inhibit
problem-solving, democracy has a large advantage over both markets and
technocratic hierarchy. The fundamental democratic commitment is to equality of
power over political decision making. Real democracies do not deliver on this
commitment any more than real markets deliver perfect competition, or real
hierarchies deliver an abstractly benevolent interpretation of rules. But a
commitment to democratic improvements is a commitment to making power
relations more equal, just as a commitment to markets is to improving
competition, and a commitment to hierarchy (in its positive aspects) is a
commitment to greater disinterestedness. This implies that a genuine commitment
to democracy is a commitment to political radicalism. We embrace this.
Democracy, then, is committed to equality of power; it is also well-suited
to exposing points of view to each other in a way that leads to identifying
better solutions. This is because democracy also involves debate. In
competitive elections and in more intimate discussions, democratic actors argue
over which proposals are better or worse, exposing their different perspectives
to each other.
Yet at first glance, this interchange of perspectives looks ugly: it is partisan, rancorous and vexatious, and people seem to never change their minds. This leads some on the left to argue that we need to replace traditional democratic forms with ones that involve genuine deliberation, where people will strive to be open-minded, and to transcend their interests. These aspirations are hopelessly utopian. Such impartiality can only be achieved fleetingly at best, and clashes of interest and perception are intrinsic to democratic politics.
Here, we concur with Jack Knight and Jim Johnson's important recent book
(2011), which argues that politics is a response to the problem of
diversity. Actors with differing --- indeed conflicting --- interests and
perceptions find that their fates are bound together, and that they must make
the best of this. Yet, Knight and Johnson argue, politics is also a matter of
seeking to harness diversity so as to generate useful knowledge. They
specifically do not argue that democracy requires impartial
deliberation. Instead, they claim that partial and self-interested debate can
have epistemological benefits. As they describe it, "democratic decision
processes make better use of the distributed knowledge that exists in a society
than do their rivals" such as market coordination or judicial decision making
(p. 151). Knight and Johnson suggest that approaches based on diversity, such
as those of Scott Page and Elizabeth Anderson, provide a better foundation for
thinking about the epistemic benefits of democracy than the arguments of
Condorcet and his intellectual heirs.
We agree. Unlike Hayek's account of markets, and Thaler and Sunstein's
account of hierarchy, this argument suggests that democracy can both foster
communication among individuals with highly diverse viewpoints. This is an
argument for cognitive democracy, for democratic arrangements that
take best advantage of the cognitive diversity of their population. Like us,
Knight and Johnson stress the pragmatic benefits of equality. Harnessing the
benefits of diversity means ensuring that actors with a very wide range of
viewpoints have the opportunity to express their views and to influence
collective choice. Unequal societies will select only over a much smaller range
of viewpoints --- those of powerful people. Yet Knight and Johnson do not
really talk about the mechanisms through which clashes between different actors
with different viewpoints result in better decision making. Without such a
theory, it could be that conflict between perspectives results in worse rather
than better problem solving. To make a good case for democracy, we not only
need to bring diverse points of view to the table, but show that
the specific ways in which they are exposed to each other have
beneficial consequences for problem solving.
There is micro-level work which speaks to this issue. Hugo Mercier and Dan
Sperber (2011) advance a purely 'argumentative' account of reasoning, on which
reasoning is not intended to reach right answers, but rather to evaluate the
weaknesses of others' arguments and come up with good arguments to support
one's own position. This explains both why confirmation bias and motivated
reasoning are rife, and why the quality of argument is significantly better
when actors engage in real debates. Experimentally, individual performance when
reasoning in non-argumentative settings is 'abysmal,' but is 'good' in
argumentative settings. This, in turn, means that groups are typically better
in solving problems than is the best individual within the group . Indeed,
where there is diversity of opinion, confirmation bias can have positive
consequences in pushing people to evaluate and improve their arguments in a
competitive setting.
When one is alone or with people who hold similar views, one's arguments will not be critically evaluated. This is when the confirmation bias is most likely to lead to poor outcomes. However, when reasoning is used in a more felicitous context — that is, in arguments among people who disagree but have a common interest in the truth — the confirmation bias contributes to an efficient form of division of cognitive labor. When a group has to solve a problem, it is much more efficient if each individual looks mostly for arguments supporting a given solution. They can then present these arguments to the group, to be tested by the other members. This method will work as long as people can be swayed by good arguments, and the results reviewed ... show that this is generally the case. This joint dialogic approach is much more efficient than one where each individual on his or her own has to examine all possible solutions carefully (p. 65).
A separate line of research in experimental social psychology (Nemeth et al. (2004), Nemeth and Ormiston (2007), and Nemeth (2012)) indicates that problem-solving groups produce more solutions, which outsiders assess as better and more innovative, when they contain persistent dissenting minorities, and are encouraged to engage in, rather than refrain from, mutual criticism. (Such effects can even be seen in school-children: see Mercer, 2000.) This, of course, makes a great deal of sense from Mercier and Sperber's perspective.
This provides micro-level evidence that political argument will improve
problem solving, even if we are skeptical about human beings' ability to
abstract away from their specific circumstances and interests. Neither a
commitment to deliberation, nor even standard rationality is required for
argument to help solve problems. This has clear implications for democracy,
which forces actors with very different perspectives to engage with each
others' viewpoints. Even the most homogenous-seeming societies contain great
diversity of opinion and of interest (the two are typically related) within
them. In a democracy, no single set of interests or perspectives is likely to
prevail on its own. Sometimes, political actors have to build coalitions with
others holding dissimilar views, a process which requires engagement between
these views. Sometimes, they have to publicly contend with others holding
opposed perspectives in order to persuade uncommitted others to favor their
interpretation, rather than another. Sometimes, as new issues arise, they have
to persuade even their old allies of how their shared perspectives should be
reinterpreted anew.
More generally, many of the features of democracy that skeptical liberals
deplore are actually of considerable benefit. Mercier and Sperber's work
provides microfoundations for arguments about the benefits of political
contention, such as John Stuart Mill's, and of arguments for the benefits of
partisanship, such as Nancy Rosenblum's (2008) sympathetic critique and
reconstruction of Mill. Their findings suggest that the confirmation bias that
political advocates have are subject to can have crucial benefits, so long as
it is tempered by the ability to evaluate good arguments in context.
Other work suggests that the macro-structures of democracies too can have
benefits. Lazer and Friedman (2007) find on the basis of simulations that
problem solvers connected via linear networks (in which there are few links)
will find better solutions over the long run than problem solvers connected via
totally connected networks (in which there all nodes are linked to each
other). In a totally connected network, actors copy the best immediately
visible solution quickly, driving out diversity from the system, while in a
linear network, different groups explore the space around different solutions
for a much longer period, making it more likely that they will identify better
solutions that were not immediately apparent. Here, the macro-level structure
of the network does the same kind of work that confirmation bias does in
Mercier and Sperber's work --- it preserves diversity and encourages actors to
keep exploring solutions that may not have immediate
payoffs.
This work offers a cognitive justification for the macro-level organization
of democratic life around political parties. Party politics tends to organize
debate into intense clusters of argument among people (partisans for the one or
the other party) who agree in broad outline about how to solve problems, but
who disagree vigorously about the specifics. Links between these clusters are
much rarer than links within them, and are usually mediated by
competition. Under a cognitive account, one might see each of these different
clusters as engaged in exploring the space of possibilities around a particular
solution, maintaining some limited awareness of other searches being performed
within other clusters, and sometimes discreetly borrowing from them in order to
improve competitiveness, but nonetheless preserving an essential level of
diversity (cf. Huckfeldt et al., 2004). Such very general considerations do not
justify any specific partisan arrangement, as there may be better (or
worse) arrangements available. What it does is highlight how party organization
and party competition can have benefits that are hard or impossible to match in
a less clustered and more homogenous social setting. Specifically, it shows how
partisan arrangements can be better at solving complex problems than
non-partisan institutions, because they better preserve and better harness
diversity.
This leads us to argue that democracy will be better able to solve complex
problems than either markets or hierarchy, for two reasons. First, democracy
embodies a commitment to political equality that the other two
macro-institutions do not. Clearly, actual democracies achieve political
equality more or less imperfectly. Yet if we are right, the better a democracy
is at achieving political equality, the better it will be, ceteris
paribus, at solving complex problems. Second,
democratic argument, which people use either to ally with or to attack
those with other points of view, is better suited to exposing different
perspectives to each other, and hence capturing the benefits of diversity, than
either markets or hierarchies. Notably, we do not make heroic claims about
people's ability to deliberate in some context that is free from faction and
self-interest. Instead, even under realistic accounts of how people argue,
democratic argument will have cognitive benefits, and indeed can transform
private vices (confirmation bias) into public virtues (the preservation of
cognitive diversity). Democratic structures --- such as political parties
--- that are often deplored turn out to have important cognitive
advantages.
Democratic experimentalism and the Internet
As we have emphasized several times, we have no reason to think that
actually-existing democratic structures are as good as they could be, or even
close. If nothing else, designing institutions is, itself, a highly complex
problem, where even the most able decision-makers have little ability to
foresee the consequences of their actions. Even when an institution works well
at one time, the array of other institutions, social and physical conditions in
which it must function is constantly changing. Institutional design and reform,
then, is unavoidably a matter of more or less ambitious "piecemeal social
experiments", to use the phrase of Popper (1957). As emphasized by Popper, and
by independently by Knight and Johnson, one of the strengths of democracy is
its ability to make, monitor, and learn from such
experiments. (Knight and Johnson particularly
emphasize the difficulty markets have in this task.) Democracies can, in fact,
experiment with their own arrangements.
For several reasons, the rise of the Internet makes this an especially
propitious time for experimenting with democratic structures themselves. The
means available for communication and information-processing are obviously
going to change the possibilities for collective decision-making. (Bureaucracy
was not an option in the Old Stone Age, nor representative democracy without
something like cheap printing.) We do not yet know the possibilities
of Internet-mediated communication for gathering dispersed knowledge, for
generating new knowledge, for complex problem-solving, or for collective
decision-making, but we really ought to find out.
In fact, we are already starting to find out. People are building systems to
accomplish all of these tasks, in narrower or broader domains, for their own
reasons. Wikipedia is, of course, a famous example of allowing lots of
more-or-less anonymous people to concentrate dispersed information about an
immense range of subjects, and to do so both cheaply and
reliably. Crucially, however, it is not
unique. News-sharing sites like Digg, Reddit, etc. are ways of focusing
collective attention and filtering vast quantities of information. Sites like
StackExchange have become a vital part of programming practice, because they
encourage the sharing of know-how about programming, with the same system
spreading to many other technical domains. The knowledge being aggregated
through such systems is not tacit, rather it is articulated and
discursive, but it was dispersed and is now shared. Similar systems are even
being used to develop new knowledge. One mode of this is open-source software
development, but it is also being used in experiments like the Polymath Project
for doing original mathematics
collaboratively.
At a more humble level, there are the ubiquitous phenomena of mailing lists,
discussion forums, etc., etc., where people with similar interests discuss
them, on basically all topics of interest to people with enough resources to
get on-line. These are, largely inadvertently, experiments in developing
collective understandings, or at least shared and structured disagreements,
about these topics.
All such systems have to face tricky problems of coordinating their
computational architecture, their social organization, and their cognitive
functions (Shalizi, 2007; Farrell and Schwartzberg, 2008). They need ways of of
making findings (or claims) accessible, of keeping discussion productive, and
so forth and so on. (Often, participants are otherwise strangers to each other,
which is at the least suggestive of the problems of trust and motivation which
will face efforts to make mass democracy more participative.) This opens up an
immense design space, which is still very poorly understood --- but almost
certainly presents a rugged search landscape, with an immense number of local
maxima and no very obvious path to the true peaks. (It is even possible that
the landscape, and so the peaks, could vary with the subject under debate.) One
of the great aspects of the current moment, for cognitive democracy, is that it
has become (comparatively) very cheap and easy for such experiments to be made
online, so that this design space can be explored.
There are also online ventures which are failures, and these, too, are
informative. They range from poorly-designed sites which never attract (or
actively repel) a user base, or produce much of value, to online groupings
which are very successful in their own terms, but are, cognitively, full of
fail, such as thriving communities dedicated to conspiracy theories. These are
not just random, isolated eccentrics,
but highly structured communities
engaged in sharing and developing ideas, which just so happen to be very
bad ideas. (See, for instance, Bell et al. (2006)
on the networks of those who share delusions that their
minds are being controlled by outside forces.) If we want to understand
what makes successful online institutions work, and perhaps even draw lessons
for institutional design more generally, it will help tremendously to contrast
the successes with such failures.
The other great aspect for learning right now is that all these experiments
are leaving incredibly detailed records. People who use these sites or systems
leave detailed, machine-accessible traces of their interactions with each
other, even ones which tell us about what they were thinking. This is
an unprecedented flood of detail about experiments with collective cognition,
and indeed with all kinds of institutions, and about how well they served
various functions. Not only could we begin to just observe successes
and failures, but we can probe the mechanisms behind those outcomes.
This points, we think, to a very clear constructive agenda. To exaggerate a
little, it is to see how far the Internet enables modern democracies to make as
much use of their citizens' minds as did Ober's Athens. We want to learn from
existing online ventures in collective cognition and decision-making. We want
to treat these ventures are, more or less, spontaneous
experiments,
and compare the success and failures (including partial successes and
failures) to learn about institutional mechanisms which work well at harnessing
the cognitive diversity of large numbers of people who do not know each other
well (or at all), and meet under conditions of relative equality, not
hierarchy. If this succeeds, what we learn from this will provide the basis for
experimenting with the re-design of democratic institutions themselves.
We have, implicitly, been viewing institutions through the lens of
information-processing. To be explicit, the human actions and interactions
which instantiate an institution also implement abstract computations
(Hutchins, 1995). Especially when designing institutions for collective
cognition and decision-making, it is important to understand them as
computational processes. This brings us to our concluding suggestions about
some of the ways social science and computer science can help each other.
Hong and Page's work provides a particularly clear, if abstract,
formalization of the way in which diverse individual perspectives or heuristics
can combine for better problem-solving. This observation is highly familiar in
machine learning, where the large and rapidly-growing class of "ensemble
methods" work, explicitly, by combining multiple imperfect models, which helps
only because the models are different (Domingos, 1999) --- in some cases it
helps exactly to the extent that the models are different (Krogh and
Vedelsby, 1995). Different ensemble techniques correspond to different
assumptions about the capacities of individual learners, and how to combine or
communicate their predictions. The latter are typically extremely simplistic,
and understanding the possibilities of non-trivial organizations for learning
seems like a crucial question for both machine learning and for social
science.
Conclusions: Cognitive Democracy
Democracy, we have argued, has a capacity unmatched among other macro-structures to actually experiment, and to make use of cognitive diversity in solving complex problems. To make the best use of these potentials, democratic structures must themselves be shaped so that social interaction and cognitive function reinforce each other. But the cleverest institutional design in the world will not help unless the resources --- material, social, cultural --- needed for participation are actually broadly shared. This is not, or not just, about being nice or equitable; cognitive diversity is itself a resource, a source of power, and not something we can afford to waste.
[Partial] Bibliography
Badii, Remo and Antonio Politi (1997). Complexity: Hierarchical Structures and Scaling in Physics, Cambridge, England: Cambridge University Press.
Bell, Vaughan, Cara Maiden, Antonio Mu{~n}oz-Solomando and Venu Reddy (2006). "``Mind Control'' Experience on the {Internet}: Implications for the Psychiatric Diagnosis of Delusions", Psychopathology, vol. 39, pp. 87--91, http://arginine.spc.org/vaughan/Bell_et_al_2006_Preprint.pdf
Blume, Lawrence Blume and David Easley (2006). "If You're so Smart, Why Aren't You Rich? Belief Selection in Complete and Incomplete Markets", Econometrica, vol. 74, pp. 929--966, http://www.santafe.edu/media/workingpapers/01-06-031.pdf
Bowles, Samuel and Suresh Naidu (2008). "Persistent Institutions", working paper 08-04-015, Santa Fe Institute, http://tuvalu.santafe.edu/~bowles/PersistentInst.pdf
Domingos, Pedro (1999). "The Role of Occam's Razor in Knowledge Discovery", Data Mining and Knowledge Discovery, vol. 3, pp. 409--425, http://www.cs.washington.edu/homes/pedrod/papers/dmkd99.pdf
Farrell, Henry and Melissa Schwartzberg (2008). "Norms, Minorities, and Collective Choice Online", Ethics and International Affairs 22:4, http://www.carnegiecouncil.org/resources/journal/22_4/essays/002.html
Hacker, Jacob S. and Paul Pierson (2010). Winner-Take-All Politics: How Washington Made the Rich Richer --- And Turned Its Back on the Middle Class. New York: Simon and Schuster.
Hayek, Friedrich A. (1948). Individualism and Economic Order. Chicago: University of Chicago Press.
Hong, Lu and Scott E. Page (2004). "Groups of diverse problem solvers can outperform groups of high-ability problem solvers", Proceedings of the National Academy of Sciences, vol. 101, pp. 16385--16389, http://www.cscs.umich.edu/~spage/pnas.pdf
Huckfeldt, Robert, Paul E. Johnson and John Sprague (2004). Political Disagreement: The Survival of Diverse Opinions within Communication Networks, Cambridge, England: Cambridge University Press.
Hutchins, Edwin (1995). Cognition in the Wild. Cambridge, Massachusetts: MIT Press.
Judd, Stephen, Michael Kearns and Yevgeniy Vorobeychik (2010). "Behavioral dynamics and influence in networked coloring and consensus", Proceedings of the National Academy of Sciences, vol. 107, pp. 14978--14982, doi:10.1073/pnas.1001280107
Knight, Jack (1992). Institutions and Social Conflict, Cambridge, England: Cambridge University Press.
Knight, Jack and James Johnson (2011). The Priority of Democracy: Political Consequences of Pragmatism, Princeton: Princeton University Press.
Krogh, Anders and Jesper Vedelsby (1995). "Neural Network Ensembles, Cross Validation, and Active Learning", pp. 231--238 in G. Tesauro et al. (eds)., Advances in Neural Information Processing Systems 7 [NIPS 1994], http://books.nips.cc/papers/files/nips07/0231.pdf
Laughlin, Patrick R. (2011). Group Problem Solving. Princeton: Princeton University Press.
Lazer, David and Allan Friedman (2007). "The Network Structure of Exploration and Exploitation", Administrative Science Quarterly, vol. 52, pp. 667--694, http://www.hks.harvard.edu/davidlazer/files/papers/Lazer_Friedman_ASQ.pdf
Lindblom, Charles (1982). "The Market as Prison", The Journal of Politics, vol. 44, pp. 324--336, http://www.jstor.org/pss/2130588
Mason, Winter A., Andy Jones and Robert L. Goldstone (2008). "Propagation of Innovations in Networked Groups", Journal of Experimental Psychology: General, vol. 137, pp. 427--433, doi:10.1037/a0012798
Mason, Winter A. and Duncan J. Watts (2012). "Collaborative Learning in Networks", Proceedings of the National Academy of Sciences, vol. 109, pp. 764--769, doi:10.1073/pnas.1110069108
Mercer, Neil (2000). Words and Minds: How We Use Language to Think Together. London: Routledge.
Mercier, Hugo and Dan Sperber (2011). "Why do humans reason? Arguments for an argumentative theory", Behavioral and Brain Sciences, vol. 34, pp.
57--111, doi:10.1017/S0140525X10000968
Mitchell, Melanie (1996). An Introduction to Genetic Algorithms, Cambridge, Massachusetts: MIT Press.
Moore, Cristopher and Stephan Mertens (2011). The Nature of Computation. Oxford: Oxford University Press.
Nelson, Richard R. and Sidney G. Winter (1982). An Evolutionary Theory of Economic Change. Cambridge, Massachusetts: Harvard University Press.
Nemet, Charlan J., Bernard Personnaz, Marie Personnaz and Jack A. Goncalo (2004). "The Liberating Role of Conflict in Group Creativity: A Study in Two Countries",
European Journal of Social Psychology, vol. 34, pp. 365--374, doi:10.1002/ejsp.210
Nemeth, Charlan Jeanne and Margaret Ormiston (2007). "Creative Idea Generation: Harmony versus Stimulation", European Journal of Social Psychology, vol. 37, pp. 524--535, doi:10.1002/ejsp.373
Nemeth, Charlan Jeanne (2012). "Minority Influence Theory", pp. 362--378 in
P. A. M. Van Lange et al. (eds.), Handbook of Theories in Social Psychology, vol. II. New York: Sage.
Page, Scott E. Page (2011). Diversity and Complexity, Princeton: Princeton University Press.
Pfeffer, Jeffrey and Robert I. Sutton (2006). Hard Facts, Dangerous Half-Truths and Total Nonsense: Profiting from Evidence-Based Management. Boston: Harvard Business School Press.
Popper, Karl R. (1957). The Poverty of Historicism, London: Routledge.
Popper, Karl R. (1963). Conjectures and Refutations: The Growth of Scientific Knowledge, London: Routledge.
Rosenblum, Nancy (2008). On the Side of the Angels: An Appreciation of Parties and Partisanship. Princeton: Princeton University Press.
Salganik, Matthew J., Peter S. Dodds and Duncan J. Watts (2006). "Experimental study of inequality and unpredictability in an artificial cultural market", Science, vol. 311, pp. 854--856, http://www.princeton.edu/~mjs3/musiclab.shtml
Shalizi, Cosma Rohilla (2007). "Social Media as Windows on the Social Life of the Mind", in AAAI 2008 Spring Symposia: Social Information Processing, http://arxiv.org/abs/0710.4911
Shalizi, Cosma Rohilla, Kristina Lisa Klinkner and Robert Haslinger (2004). "Quantifying Self-Organization with Optimal Predictors", Physical Review Letters, vol. 93, art. 118701, http://arxiv.org/abs/nlin.AO/0409024
Shalizi, Cosma Rohilla Shalizi and Andrew C. Thomas (2011). "Homophily and Contagion Are Generically Confounded in Observational Social Network Studies", Sociological Methods and Research, vol. 40, pp. 211--239, http://arxiv.org/abs/1004.4704
Shapiro, Carl and Hal R. Varian (1998). Information Rules: A Strategic Guide to the Network Economy, Boston: Harvard Business School Press
Stiglitz, Joseph E. (2000). "The Contributions of the Economics of Information to Twentieth Century Economics", The Quarterly Journal of Economics, vol. 115, pp. 1441--1478, http://www2.gsb.columbia.edu/faculty/jstiglitz/download/papers/2000_Contributions_of_Economics.pdf
Sunstein, Cass R. (2003). Why Societies Need Dissent. Cambridge, Massachusetts: Harvard University Press.
Swartz, Aaron (2006). "Who Writes Wikipedia?", http://www.aaronsw.com/weblog/whowriteswikipedia
Posted by crshalizi at May 23, 2012 15:00 | permanent link